Выполненные работы ФизикаСанкт-Петербургский Государственный Университет Телекоммуникаций им проф. М.А.Бонч-БруевичаГотовые решения задач по физике для студентов СПБГУТ. Помощь студенту СПБГУТ в решении контрольных и лабораторных работ по физике.
Учебные материалы |  | Методичка 1993 часть 3 |  |
| | Министерство связи РФ
Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича
Методические указания по организации самостоятельной работы и контрольные задания по общему курсу ФИЗИКИ для студентов заочного факультета
Часть III
Санкт-Петербург 1993
Стоимость решения одной задачи по физике уточняйте при заказе.
Готовы следующие варианты:
Вариант 02
Задача 5.3
Установка для наблюдения колец Ньютона освещается падающим нормально монохроматическим светом с длинной волны 5600Ǻ. Радиус кривизны линзы 2 м. Определить: расстояние между вторым и третьим светлыми кольцами Ньютона в проходящем свете, разность толщины воздушного клина в местах образования этих колец.
Задача 5.10
Дифракционная решетка длиной L = 2,5см имеет 4*10^3 штрих/см. Определить разрешающую способность решётки в спектре третьего порядка; наименьшую разность длин волн двух спектральных линий одинаковой интенсивности вблизи 0,56 мкм, которые можно разрешить при помощи этой решётки в максимальном порядке спектра, если параллельный пучок света падает на решётку нормально.
Задача 5.15
Луч света последовательно проходит через два николя, главные оптические плоскости которых образуют угол 50. Поглощение в каждом николе составляет 10% падающего света. Определить, во сколько раз луч, выходящий из второго николя, ослаблен по сравнению с лучом, падающим на первый николь.
Задача 5.17
Две частицы с одинаковыми скоростями 3с /4 движутся по одной прямой и попадают в мишень. Одна из частиц попала в мишень позже другой на время 10^-8с. Определить расстояние между частицами в полёте в системе отсчёта, связанной с ними.
Задача 5.23
Вследствие повышения температуры максимум излучательной способности абсолютно черного тела r переместился с длины волны 2∙10-6 м на длину волны 10^-6 м. Определить во сколько раз изменилась интегральная светимость.
Задача 5.28
Фотоэлектроны вылетают из цинка при освещении его электромагнитным излучением с длинной волны 0,2∙10^-6 м. Работа выхода электрона с цинка равна 4 эВ. Определить: максимальные энергию и скорость фотоэлектронов; энергию, импульс и массу фотона падающего излучения.
Задача 5.33
Определить скорость электрона на второй орбите в атоме водорода и работу, которую нужно совершить, чтобы удалить электрон с этой орбиты за пределы влияния его ядра.
Задача 5.38
Определить ускоряющую разность потенциалов, которую должен пройти электрон, чтобы его длина волны де Бойля стала равной м.
Начальную скорость электрона считать равной нулю.
Вариант 04
Задача 5.5
Установка для наблюдения колец Ньютона в отраженном свете освещается падающим нормально монохроматическим светом с длиной волны 5*10(3) А. Первоначально пространство между линзой и стеклянной пластинкой заполнено водой (n=1.33). После того, как его заполнили сероуглеродом, радиус третьего светлого кольца Ньютона уменьшился в 1,1 раза. Радиус кривизны линзы равен 2 м. Определить: толщину слоя воды в месте наблюдения третьего светлого кольца; показатель преломления сероуглерода, если известно, что он меньше показателя преломления стекла.
Задача 5.9
На дифракционную решетку, имеющую 500 штрихов на 1мм, нормально к поверхности падает параллельный пучок лучей. Определить: угол отклонения луча для линии 6500 А в спектре третьего порядка; длину волны спектральной линии, изображение которой, даваемое этой дифракционной решеткой в спектре четвертого порядка, совпадает с данной линией.
Задача 5.14
Угол между главными плоскостями поляризатора и анализатора равен 45 градусам. Во сколько раз уменьшится интенсивность света, выходящего из анализатора, если угол увеличить до 60 градусов? Сделайте чертеж. Выведите расчетную формулу.
Задача 5.19
Определить, какую ускоряющую разность потенциалов должна пройти частица, чтобы ее скорость составила 95% скорости света. Задачу решить для: электронов; протонов.
Задача 5.25
Энергия фотона, соответствующего максиму излучательной способности абсолютно черного тела, равна 3,3*10(-20) Дж. Определить энергетическую светимость этого тела.
Задача 5.26
Катод освещается излучением с длиной волны 3600 А, причем ежесекундно на 1 см2 поверхности падает энергия 6∙10-5 Дж. Считается, что 3% падающих фотонов выбивают электроны. Определить: плотность тока насыщения, получаемого с фотокатода; давление, которое оказывает на катод падающее нормально излучение, если коэффициент отражения 0,2.
Задача 5.35
Определить, какую наименьшую скорость должны иметь электроны, чтобы произвести ионизацию атома водорода.
Задача 5.40
Определить, насколько изменится длина волны де Бройля электрона, вырванного квантом с энергией 14,5 эВ с первой боровской орбиты атома водорода на большое расстояние.
Вариант 06
Задача 5.4
Установка для наблюдения колец Ньютона освещается падающим нормально монохроматическим светом. Наблюдение ведётся в отражённом свете. Радиусы двух соседних тёмных колец равны соответственно 4 мм и 4,38мм. Радиус кривизны линзы 5м. Определить: порядковые номера колец; разность толщин воздушного клина в местах образования этих колец; длину волны падающего света.
Задача 5.7
На диафрагму с отверстием радиусом 1мм падает сферическая волна ( 5000А). В точке А находится точечный источник, в точке В находится наблюдатель. Расстояние от источника до наблюдателя 2м. Диафрагма перемещается из точки отстоящей от А на 1м, в точку, отстоящую от А на 1,75м. Определить, сколько раз будет наблюдаться затемнение в точке В.
Задача 5.12
Предельный угол полного внутреннего отражения пучка света для некоторого вещества равен 450. Чему равен для этого вещества угол полной поляризации.
Задача 5.20
Определить, какую ускоряющую разность потенциалов должна пройти альфа частица, чтобы её продольные размеры стали меньше в два раза.
Задача 5.24
Температура абсолютно чёрного тела равна 4000К. Определить число фотонов, которое испускало бы это тело ежесекундно с 1см2 поверхности, если бы все фотоны соответствовали длине волны, на которую приходится максимум излучательной способности этого тела.
Задача 5.29
Определить постоянную Планка, если известно, что фотоэлектроны, вырываемые с поверхности некоторого металла светом с частотой 2,2*1015с-1, полностью задерживаются обратным потенциалом 6,6В, а красная граница фотоэффекта для этого металла 5*10-7м
Задача 5.34
Найти наименьшую и наибольшую длины волн спектральных линий серии Бальмера. Определить соответствующие частоты излучения и энергию фотонов.
Задача 5.37
Определить, какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 1А до 0,5А?
Вариант 07
Задача 5.3
Установка для наблюдения колец Ньютона освещается падающим нормально монохроматическим светом с длинной волны 5600Ǻ. Радиус кривизны линзы 2 м. Определить: расстояние между вторым и третьим светлыми кольцами Ньютона в проходящем свете, разность толщины воздушного клина в местах образования этих колец
Задача 5.8
Дифракционная решетка имеет 50 штрихов на 1 мм. Пучок параллельных лучей падает нормально на поверхность решетки. Определить, какова должна быть длина решетки, что бы в спектре второго порядка разрешить две линии натрия с длинами волн 5890Ǻ и 5896Ǻ; наибольший порядок спектра, наблюдаемый для линии 5890Ǻ; угловую дисперсию в этом порядке для линии 5890Ǻ.
Задача 5.11
На стеклянную пластинку с показателем преломления 1,54 падает естественный луч света. Отраженный луч максимально поляризован. Определить: угол между падающим и отраженным лучами; угол преломления.
Задача 5.18
Скорость электрона составляет 0,9с. Определить относительную ошибку ΔТ/Т в определении кинетической энергии электрона, если эта энергия будет вычислена по формуле mυ2/2.
Задача 5.23
Вследствие повышения температуры максимум излучательной способности абсолютно черного тела r переместился с длины волны 2∙10^-6 м на длину волны 10-6 м. Определить во сколько раз изменилась интегральная светимость.
Задача 5.28
Фотоэлектроны вылетают из цинка при освещении его электромагнитным излучением с длинной волны 0,2∙10^-6 м. Работа выхода электрона с цинка равна 4 эВ. Определить: максимальные энергию и скорость фотоэлектронов; энергию, импульс и массу фотона падающего излучения.
Задача 5.32
Атом водорода, находящийся в нормальном состоянии, переведен в возбужденное состояние, характеризующее квантовым числом 3. Определить энергию возбуждения атома и радиус орбиты.
Задача 5.38
Определить ускоряющую разность потенциалов, которую должен пройти электрон, чтобы его длина волны де Бройля стала равной 10(-10) м. Начальную скорость электрона считать равной нулю.
Вариант 08
Задача 5.2
Плоско – выпуклая стеклянная линза (1,6) оптическая сила которой 0,1дптр, лежит на пластинке из стекла. Установка освещается падающим нормально монохроматическим светом с длиной волы 0,6мкм. Определить: толщину воздушного зазора там, где в отражённом свете наблюдается первое светлое кольцо Ньютона; радиус этого кольца.
Задача 5.9
На дифракционную решетку, имеющую 500 штрихов на 1мм, нормально к поверхности падает параллельный пучок лучей. Определить: угол отклонения луча для линии в спектре третьего порядка; длину волны спектральной линии, изображение которой, даваемое этой дифракционной решеткой в спектре четвертого порядка, совпадает с данной линией.
Задача 5.13
Угол полной поляризации при отражении света от поверхности некоторого изотропного вещества равен 56020. Определите скорость света в этом веществе.
Задача 5.17
Две частицы с одинаковыми скоростями 3с /4 движутся по одной прямой и попадают в мишень. Одна из частиц попала в мишень позже другой на время 10^-8с. Определить расстояние между частицами в полёте в системе отсчёта, связанной с ними.
Задача 5.22
Исследование спектра излучения Солнца показывает, что максимум его излучательной способности соответствует длине волны 5*10^-7м Принимая Солнце за черное тело, определить : 1) энергетическую светимость Солнца;
2) поток энергии, излучаемый Солнцем.
Задача 5.27
Кванты света с энергией 4,9эВ вырывают фотоэлектроны из металла с работой выхода 4,5 эВ. Свет падает на поверхность металла по нормали. Определить : максимальный суммарный импульс, передаваемый поверхности металла при вылете каждого электрона; задерживающую разность потенциалов.
Задача 5.33
Определить скорость электрона на второй орбите в атоме водорода и работу, которую нужно совершить, чтобы удалить электрон с этой орбиты за пределы влияния его ядра.
Задача 5.39
Электрон, движущийся со скоростью 5*106м/с, попал в ускоряющее поле с напряженностью 103В/м. Какое расстояние он прошел в поле, если длина волны де Бройля стала равна 1 А0.
Вариант 09
Задача 5.1
Установка для наблюдения колец Ньютона освещается падающим нормально монохроматическим светом с длиной волны 0,6 мкм. Радиус кривизны линзы 1 м, оптическая сила 0,6 дптр. Определить: показатель преломления материала, из которого изготовлена линза; радиус четвертого темного кольца Ньютона в отраженном свете; толщину воздушного слоя между линзой и стеклянной пластинкой в том месте, где оно наблюдается.
Задача 5.10
Дифракционная решетка длиной 2,5 см имеет 4*10(3) штрихов на 1 см. Определить: разрешающую способность дифракционной решетки для спектра третьего порядка.
Задача 5.15
Луч света последовательно проходит через два николя, главные оптические плоскости которых образуют угол 50. Поглощение в каждом николе составляет 10% падающего света. Определить, во сколько раз луч, выходящий из второго николя, ослаблен по сравнению с лучом, падающим на первый николь.
Задача 5.19
Определить, какую ускоряющие разность потенциалов должна пройти частица, чтобы ее скорость составила 95% скорости света. Задачу решить для: электронов; протонов.
Задача 5.21
Абсолютно черное тело излучает с 1 см2 в минуту 2226 Дж энергии. Определить, температуру абсолютно черного тела; длину волны, на которую приходится максимум его излучательной способности.
Задача 5.26
Катод освещается излучением с длиной волны 3600 А, причем ежесекундно на 1 см2 поверхности падает энергия 6*10(-5) Дж. Считается, что 3% падающих фотонов выбивают электроны. Определить плотность тока насыщения, получаемого с фотокатода; давление, которое оказывает на катод падающее нормально излучение, если коэффициент отражения 0,2.
Задача 5.31
Первоначально покоившийся атом водорода испустил фотон, соответствующий головной линии серии Лаймана. Определить скорость, которую приобрел атом.
Задача 5.40
Определить, насколько изменится длина волны де Бройля электрона, вырванного квантом с энергией 14,5 эВ с первой боровской орбиты атома водорода на большое расстояние.
|  |  | Методичка 1997 часть 1 |  |
| |
Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича
Курс физики
Методические указания и контрольные задания
Факультет вечернего и заочного обучения
Часть 1
Санкт-Петербург
1997
Готовые задач по физике можно приобрести онлайн.
Стоимость одной готовой задачи по физике указана напротив каждой задачи.
Стоимость выполнения на заказ уточняйте при заказе.
Решение подробно расписано в формате Word. На почту высылаем файл word + копию в pdf.
Выполнены следующие задачи
(можно купить решенные ранее задания по основам теории управления онлайн и мгновенно получить на email)
Зависимость скорости от времени прямолинейно движущегося тела задана уравнением v=s+2t2 (м/с). Масса тела 1кг. Определить: среднее ускорение за первые 2с движения; силу, приложенную к телу в момент времени t = 3с; путь, пройденный телом за промежуток времени от t1 = 1с до t2 = 2с.
Импульс тела массой 0,5кг движущегося прямолинейно, изменяется по закону p=2+3t+4t2 (кг·м/с).
Определить: скорость и ускорение тела в момент времени t = 2с; работу силы за промежуток времени от t1 = 2с до t2 = 3с; величину силы, приложенной к телу в момент времени 2с.
Зависимость пути, пройденного прямолинейно движущимся телом, от времени дается уравнением S = 2t - 3t2 + 4t3 (м). Масса тела 2 кг.
Определить: через какой промежуток времени от начала движения импульс тела будет равен 16 кг·м/с; чему равна средняя скорость за этот промежуток времени; величину силы, действующей на тело в момент времени t = 2 с.
Камень массой 0,2 кг, летящий горизонтально со скоростью 15 м/с, ударяется о стену. В результате удара его скорость становится 10 м/с, а направление движения составляет угол 60° с первоначальным. Определить: импульс силы, полученной стенкой за время удара; работу силы взаимодействия камня со стенкой.
Деревянный шар массой 4 кг подвешен на невесомой нерастяжимой нити длиной 4 м. Пуля массой 10 г, летящая горизонтально, попадает в шар и застревает в нем. Нить отклоняется от вертикали на максимальный угол 15 градусов. Определить начальную скорость пули. Считать, что радиус шара много меньше длины нити.
Груз массой 1 кг падает на чашку пружинных весов с высоты 0,5 м. Каким будет максимальное показание весов, если после успокоения чашка весов опускается на 2 см. Массами чашки и пружины пренебречь.
Человек массой 60 кг стоит на льду. Человек бросает горизонтально камень массой 4 кг со скоростью 5 м/с. На какое расстояние откатится человек, если коэффициент трения о лёд 0,02.
Колесо радиуса 0,2 м с равномерно распределённой по ободу массой 5 кг вращается относительно неподвижной оси, перпендикулярной его плоскости и проходящей через его центр, так, что зависимость угла поворота колеса от времени задаётся уравнением φ = 5+4t2+t3 (рад). Определить: для момента времени 1 с: момент импульса колеса; момент действующей силы; кинетическую энергию колеса.
Зависимость углового ускорения колеса, вращающегося относительно неподвижной оси, перпендикулярной к его плоскости и проходящей через его центр, от времени задана уравнением ε = 2+3t2 (c-2).
Радиус колеса 0,3м, масса 20кг равномерно распределена по ободу.
Определить: угловой путь, пройденный за время от t1 =1с до t2 = 3; полное число оборотов, сделанных колесом за это время; линейную скорость точек на ободе колеса; момент импульса колеса в момент времени 3 с (при t = 0 ω = 0)
Обруч, масса которого 1 кг равномерно распределена по ободу, вращается относительно оси, перпендикулярной его плоскости и проходящей через его центр. Радиус обруча 0,1 м. Зависимость момента импульса обруча от времени имеет вид L = 0,05t2(кг·м2/с).
Материальная точка массой 2·10-3кг движется по окружности радиусом 2м. Её угловая скорость зависит от времени согласно уравнению ω = 0,4t2 (c-1).
Определить для момента времени t = 2 с: силу, действующую по касательной к траектории; нормальное, касательное и полное ускорение точки; кинетическую энергию.
Деревянный стержень массой 2 кг и длиной 1 м, расположенный горизонтально, может вращаться относительно вертикальной оси, проходящей через его конец. В другой конец стержня попадает пуля массой 0,02 кг, летящая со скоростью 600 м/с горизонтально, перпендикулярно стержню. Определить скорость, с которой будет вращаться стержень, если пуля застрянет в нём. Пулю можно считать материальной точкой.
На горизонтальной платформе, вращающейся вокруг вертикальной оси, проходящей через ее центр, стоит человек и держит на вытянутых руках две одинаковые гири массой по 2 кг каждая, при этом расстояние от оси платформы до каждой гири 0,75 м. Платформа вращается, делая 1 об/с. Человек сближает гири так, что их расстояние до оси платформы становится равным 0,4 м, а частота оборотов увеличивается до 1,2 об/с. Определить момент инерции платформы с человеком, считая его постоянным, а гири материальными точками.
Платформа в виде диска вращается по инерции вокруг вертикальной оси с частотой n1 = 15 оборотов в минуту. На краю платформы стоит человек. Когда он перешел в центр платформы, частота вращения возросла до 25 оборотов в минуту. Масса человека m = 70 кг. Определить массу платформы M. Человека считать точечной массой.
Шар и диск имеют одинаковую массу и катятся по горизонтальной поверхности без скольжения с одинаковой постоянной скоростью. Кинетическая энергия шара 70 Дж.
Определить: кинетическую энергию диска; расстояние, которое пройдут диск и шар до полной остановки если на них начнёт действовать постоянная сила сопротивления 5 Н.
Горизонтальный стержень длиной 0,8 м и массой 1,5 кг вращается относительно вертикальной оси, проходящей через его конец, с угловой скоростью 50 с-1. В некоторый момент времени к свободному концу стержня приложена тормозящая сила 3,2Н, линия действия которой горизонтальна и составляет угол 30° с осью стержня (рис.4).
Определить: число оборотов, сделанных стержнем за 10с действия силы; момент импульса стержня через 10с после начала действия силы.

Две гири, массами 2 кг и 3 кг соединены невесомой нерастяжимой нитью, перекинутой через блок, массой 1 кг. Блок является однородным диском.
Определить: ускорение, с которым движутся гири; силы натяжения нитей; кинетическую энергию системы через 1 с после начала движения.
Двум одинаковым маховикам, находящимся в покое, сообщили одинаковую угловую скорость 63 рад/с и предоставили их самим себе. Под действием сил трения один маховик остановился через одну минуту, а второй сделал до полной остановки 360 оборотов.
Определить: для какого маховика тормозящий момент сил трения больше и во сколько раз?
Обруч, вся масса которого распределена равномерно по его окружности, катится по горизонтали со скоростью 2 м/с.
Определить: какое расстояние он прокатится вверх по наклонной плоскости до полной остановки, если угол наклона плоскости к горизонту 5 градусов.
Электрический диполь образован зарядами q1=10-9 Кл и q2=-10-9 Кл, расположенными на расстоянии 2 см в воздухе.
Определить напряженность и потенциал поля в точках на перпендикуляре, восстановленном из середины диполя, на расстоянии 2 см и 30 см от диполя.
Два точечных заряда – 10-9 Кл и 2·10-9 Кл находятся на расстоянии 30 см друг от друга.
На каком расстоянии от первого заряда на прямой, проходящей через заряды, находится точка, в которой потенциал равен нулю? Какова напряжённость поля в этой точке?
Бесконечная равномерно заряженная нить и шар расположены как показано на рис.8. Заряд шара 10-9 Кл; линейная плотность заряда на нити 5·10-10 Кл/см; а = 10см. Окружающая среда – воздух. Определить напряжённость поля в точках А и В; работу поля по перемещению заряда 10-8 Кл из точки А в точку В. Считать, что расположение зарядов не нарушено.

Бесконечная плоскость, заряженная с поверхностной плотностью 10-11 Кл/см2, и шар, заряд которого 10-8 Кл, расположены, как показано на рис.9; а = 20 см. Окружающая среда - воздух. Определить: напряженность поля в точках А и В; работу перемещения заряда 10-7 Кл из точки А в точку В. Считать, что распределение зарядов не нарушено взаимодействие.

Два бесконечных равномерно заряженных цилиндра расположены так, как показано на рис.8 (ось правого цилиндра перпендикулярна плоскости чертежа). Линейная плотность заряда правого цилиндра равна - 10-7 Кл/см; линейная плотность заряда левого цилиндра 10-7 Кл/см; а = 10 см. Окружающая среда воздух. Определить: напряжённость поля в точках А и В; работу перемещения заряда 10-8 Кл из точки А в точку В. Считать, что распределение зарядов не нарушено взаимодействием.

Бесконечно большая плоскость и длинная нить расположены, как показано на рис.11 (перпендикулярно плоскости чертежа); а= 20 см; σ = 10-6 Кл/м2, τ = 10-6 Кл/м. Определить: напряжённость поля в точках А и В; работу перемещения заряда 10-7 Кл из точки А в точку В. Считать, что распределение зарядов не нарушено взаимодействием.
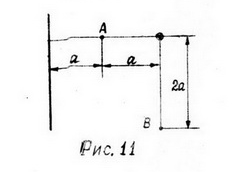
Потенциал электростатического поля задан выражением
 , где а = b = c = 0,1 м. , где а = b = c = 0,1 м.
Определить напряжённость электростатического поля в точке с координатами x = 0,2м, y = -0,2 м, z = 0,1 м.
Потенциал электростатического поля задан выражением
 , где а = 0,1 м, b = 0,2 м. , где а = 0,1 м, b = 0,2 м.
Определить напряженность электростатического поля в точке с координатами x = y = 0,2 м, z = 0,1 м.
Потенциал электростатического поля задан выражением
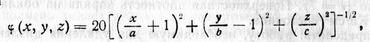 , где а = 0,2м ; b = 0,1м; с = 0,3м. , где а = 0,2м ; b = 0,1м; с = 0,3м.
Определить напряжённость электростатического поля в точке с координатами x = y = z = 0,2м.
Поток электронов, имеющих энергию 200 эВ, влетает в поле плоского воздушного конденсатора. Скорость электрона перпендикулярна силовым линиям поля. Плотность заряда на обкладках конденсатора 5·10-11 Кл/см2.
Определить: смещение электронов вдоль поля за 10-8 с движения в поле; скорость электронов через 10-8 с движения в поле.
Поток электронов движется к заряженному шару радиусом 1 см в радиальном направлении.
Какую линейную скорость должен иметь электрон на расстоянии 1 м от центра шара, чтобы достичь его поверхности, если поверхностная плотность заряда на шаре равна -10-10 Кл/м2? Определить ускорение электронов на расстоянии 0,5 м от центра шара.
Электрон движется в радиальном направлении к заряженному цилиндру радиусом 1 см.
Какую минимальную скорость должны иметь электроны на расстоянии 1 м от оси цилиндра, чтобы достичь его поверхности, если линейная плотность заряда равна — 10-10 Кл/м? Определить ускорение электрона на расстоянии 0,5 м от оси цилиндра.
Плоский воздушный конденсатор заряжен до разности потенциалов 300 В и отключен от источника. Расстояние между пластинами 0,5 см, площадь пластин 400 см2. Пластины раздвигаются до расстояния 2,5 см.
Определить: объёмную плотность энергии поля конденсатора до и после раздвижения пластин.
Пластины плоского конденсатора имеют площадь 100 см2. Расстояние между пластинами 0,5 мм. Диэлектрик стекло (ε = 7). Поверхностная плотность заряда на обкладках 10-10 Кл/см2 постоянна.
Определить: работу, необходимую для удаления диэлектрика из конденсатора; объёмную плотность энергии поля до и после удаления диэлектрика.
Сферический конденсатор состоит из двух концентрических обкладок радиусами 10 см и 14 см, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью равной 6. Конденсатор заряжен до напряжения 100 В.
Определить энергию, заключённую между сферическими поверхностями радиусами 11 см и 13 см.
Цилиндрический конденсатор состоит из двух коаксиальных обкладок высотой по 10 см и радиусами 2 см и 5 см, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью равной 7. Конденсатор заряжен до напряжения 200 В.
Определить энергию, заключенную между цилиндрическими поверхностями коаксиальными с осью конденсатора высотой 10 см и радиусами 3 см и 4 см.
Плоский конденсатор заряжен до разности потенциалов 300 В и отключен от источника. Расстояние между пластинами 5 мм, их площадь 300 см2.
Определить заряд и энергию конденсатора, если при извлечении диэлектрика из конденсатора его энергия увеличивается в 8 раз.
Между обкладками цилиндрического конденсатора (рис. 12) находятся два слоя диэлектрика: стекло (ε1 = 7) и масло (ε2 = 5). Заряд конденсатора 10-8 Кл, длина 0,1 м R1 = 5 см, R2 = 7 см, R3 = 9 см.
Определить напряжённость и электрическое смещение (индукцию) в точках на расстоянии r1 = 6 см, r2 = 8 см от оси конденсатора.

Пространство между пластинами плоского конденсатора заполнено диэлектриком с диэлектрической проницаемостью равной 4. Расстояние между пластинами конденсатора 5мм, разность потенциалов 4 кВ, площадь пластин 200 см2.
Определить: поверхностную плотность заряда на пластинах и на диэлектрике; работу поляризации диэлектрика.
Скорость упорядоченного движения электронов в проводнике возрастает со временем по закону V(t) = 2·10-4t (м/с). Удельное сопротивление проводника ρ = 10-4 Ом·см. Концентрация электронов в проводнике n = 2,5·1022 см-3. Площадь поперечного сечения проводника s = 4 мм2.
Определить: напряженность электрического поля в проводнике в момент времени t = 2 с; заряд, прошедший через сечение проводника за время от t1 = 2 с до t2 = 4 с
Разность потенциалов на концах проводника длиной l = 3 м меняется по закону U(t) = 6·10-2t2 (В). Удельное сопротивление проводника ρ = 10-4 Ом·cм. Площадь поперечного сечения s = 9 мм2.
Определить: плотность тока в проводнике в момент времени t = 2 с; количество тепла, выделившееся в проводнике при пропускании тока за промежуток времени от t1 = 1 с до t2 = 2с
В 1 м3 некоторого проводника (ρ = 10-4 Ом·см) длиной 2 м за 2 с выделяется количество тепла Q = 8·106Дж.
Определить: напряжение на концах проводника; скорость упорядоченного движения и подвижность электронов в проводнике, считая концентрацию электронов n = 1022см-3.
К источнику с внутренним сопротивлением r = 0,1 Ом подсоединена катушка из нихромового провода (ρ = 4·10-4 Ом·см. Сечение провода s = 1 мм2. Длина провода l = 10 м. Удельная мощность (количество тепла, выделяемое в 1 м3 за 1 с) ω = 106 Вт/м3.
Определить: ЭДС источника; подвижность электронов в проводе, считая концентрацию электронов n = 1022 см-3.
К источнику с ЭДС 8 В и внутренним сопротивлением 2 Ом присоединена катушка из нихромового провода (ρ = 10-4 Ом·см). Длина провода 20 м. Сечение провода 1 мм2.
Определить: скорость упорядоченного движения электронов в проводе, считая концентрацию n = 1022 см-3; КПД электрической цепи.
В 1 см3 провода (ρ = 10-4 Ом·см) за 2 мин выделяется количество тепла Q = 480 Дж.
Определить: напряженность электрического поля в проводе; скорость упорядоченного движения электронов, считая концентрацию электронов n = 1022 см-3; подвижность электронов в проводе.
ЭДС источника E' = 10 В. К источнику присоединена катушка из никелинового провода (ρ = 4·10-5 Ом·см) длиной 10 м. КПД такой цепи 80%.
Определить: скорость упорядоченного движения электронов, считая концентрацию электронов в проводе n = 2,5·1022 см-3; количество тепла, которое выделяется в 1 см3 провода за 1 мин.
В воздухе, находящемся между пластинами плоского конденсатора, в каждую секунду создаётся 100 пар ионов в 1 см3.
Определить при динамическом равновесии сопротивление слоя воздуха, заключённого между пластинами, в слабом электрическом поле. Площадь пластин 200 см2, расстояние между ними 1 см. Подвижность ионов воздуха μ+ = 1,9 см2/Вс; μ- = 1,37 см2/Вс. Ионы одновалентны. Коэффициент рекомбинации 1,6·10-6 см3·с-1.
Концентрация ионов, обусловливающих проводимость атмосферного воздуха, в среднем равна 700 см-3. Средняя величина напряженности земного электрического поля равна 130 В/м. Ионы одновалентны. Вычислить плотность тока проводимости в атмосфере. Подвижность ионов: μ+= 1,37 см2/В·с;
μ-= 1,91 см2/В·с
|  |  | Методичка 1997 часть 2 |  |
| |
Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича
Курс Физики
Методические указания т контрольные задания факультет вечернего и заочного обучения Часть II
Санкт-Петербург 1997
Готовые задачи по физике можно приобрести онлайн.
Стоимость одной готовой задачи по физике указана напротив каждой задачи.
Стоимость выполнения на заказ уточняйте при заказе.
Решение подробно расписано в формате Word. На почту высылаем файл word + копию в pdf.
Выполнены следующие задачи
(можно купить решенные ранее задания по физике онлайн и мгновенно получить на email)
Электрон, ускоренный разностью потенциалов 20 кВ, влетает в однородное магнитное поле с напряженностью 8·104 А/м. Вектор скорости образует угол 60° с направлением вектора напряженности. Определить радиус и шаг винтовой линии, по которой будет двигаться электрон.
Альфа-частица движется в однородном магнитном поле с напряженностью 9,5·105 А/м по окружности радиусом 25 см в плоскости, перпендикулярной силовым линиям. Определить: скорость частицы; период обращения частицы по окружности.
Электрон с энергией 100 эВ влетает в поперечное электрическое поле с напряженностью 60 кВ/м. Определить величину и направление напряженности магнитного поля, которое нужно создать, чтобы скорость электрона осталась неизменной.
Чему равны и во сколько раз отличаются радиусы окружностей, по которым в однородном поперечном магнитном поле индукцией 10-2Тл движутся электрон и протон, обладающие одинаковой энергией 100 эв. Масса протона в 1837 раз больше массы электрона
Внутренний диаметр области магнитного поля типичного циклотрона 1 м. Индукция магнитного поля в нем 1 Тл. Ускоряющее напряжение 100 кВ. Определить максимальную энергию, до которой могут быть ускорены в этом циклотроне протоны и скорость, приобретаемую протонами к концу ускорения.
Пластинка полупроводника толщиной а = 0,2 мм помещена в магнитное поле, направленное вдоль а. Удельное сопротивление полупроводника ρ = 10-5 Ом·м и индукция магнитного поля B = 1 Тл. Перпендикулярно полю вдоль пластинки пропускается ток I = 0,1 А. При этом возникает поперечная разность потенциалов U = 3,25·10-3 В (эффект Холла). Определить подвижность носителей тока в полупроводнике.
При измерении эффекта Холла в натриевом проводнике напряженность поперечного поля оказалась E = 5 мкВ/см при плотности тока j = 200 А/см2 и индукции магнитного поля B = 1 Тл. Найти концентрацию электронов проводимости и ее отношение к концентрации атомов в данном проводнике.
По медной пластине длиной 10 см, шириной 2 см и толщиной 1 мм протекает электрический ток силой 4 А. Разность потенциалов при этом на концах пластины равна 5·10-4 В. Если, не выключая тока, поместить пластину в перпендикулярное ей (параллельное короткой стороне) однородное магнитное поле с индукцией 0,1 Тл, то на противоположных боковых гранях возникнет холловская разность потенциалов 5·10-8 В. Определить концентрацию свободных электронов в меди и их подвижность.
В установке для наблюдения эффекта Холла медная пластина имеет размеры: длина 5·10-2 м, ширина 1 см, толщина 0,1 мм. Определить силу тока, текущего по пластине, и подвижность электронов, если при включении однородного магнитного поля с индукцией 0,32 Тл на боковых гранях пластины возникает разность потенциалов 10-6 В. Концентрация электронов в меди 8·1028 м-3, удельное сопротивление 1,7·10-8 Ом·м.
По пленке, помещенной в установку для наблюдения эффекта Холла, протекает ток силой 4,8 А. Индукция магнитного поля, в которое помещен образец, 0,2 Тл. Определить холловскую разность потенциалов и скорость упорядоченного движения электронов, считая концентрацию электронов равной 1029 м-3. Ширина пленки 2·10-3 м, толщина 10-4 м
По двум тонким проводам, один из которых горизонтально закреплён, а другой подвешен к первому на двух пружинах протекают токи одинакового направления. Найти расстояние между проводами, если длина пружин в нерастянутом состоянии 30 см, их жёсткость 10 Н/м , массы проводов по 100 г, длина 200 м, сила тока в них 100 А и 150 А.
На каком расстоянии друг от друга следует расположить провода сверхпроводящей двухпроводной линии постоянного тока, чтобы сила магнитного взаимодействия уравновесила вес нижнего провода. Сила тока в проводах 600 А и 800 А, сечение проводов 3 мм2, плотность материала 8,0·103кг/м3.
В цепи, сопротивление которой 0,2 Ом, имеется участок прямого провода длиной 0,2м, находящийся во внешнем магнитном поле индукцией 1 Тл. Определить силу, которую нужно приложить к проводу, чтобы перемещать его под углом 30° к линиям индукции магнитного поля со скоростью 0.5 м/с.
В однородном магнитном поле, индукция которого 0,1 Тл, равномерно с частотой 4 Гц вращается рамка площадью 100 см2. Сопротивление рамки 16 Ом, число витков рамки 100. Определить максимальное значение мощности, которую необходимо приложить к рамке для осуществления такого вращения.
Медный провод массой 178 г намотан на круглую рамку диаметром 0,141 м, которая вращается во внешнем однородном магнитном поле, индукция которого 1 Тл, с частотой 5 Гц. Определить действующее значение ЭДС в рамке и мощность, выделяющуюся во внешней цепи на сопротивлении 9,86 Ом. Плотность меди 8,9·103 кг/м3. Площадь сечения провода 1 мм2.
По двум длинным параллельным проводам, расположенным на расстоянии 10 см один от другого, идут токи 3 А и 7 А противоположных направлениях. Определить напряженность магнитного поля в точке, находящейся на расстоянии 8 см от одного провода и, одновременно, на расстоянии 10 см от другого провода.
Длинный провод, согнутый под прямым углом, и круговой контур расположены в одной плоскости, как показано на рис. Цент кругового контура находится на биссектрисе прямого угла. I1 = 10А; I2 = 1А; а = 10см; R = 5см. Определить напряжённость магнитного поля в центре кругового контура.

Длинный провод с током 5А согнут под прямым углом и расположен в плоскости чертежа. На расстоянии 14см от вершины угла С в точке В, равноудалённой от обеих сторон угла, перпендикулярно плоскости чертежа расположен второй провод с током 4А. Определить напряжённость магнитного поля в точке А, находящейся на расстоянии а/2 от вершины угла С.
Квадратный контур и круговой контур с радиусом 5см расположены во взаимно перпендикулярных плоскостях, как показано на рисунке. По квадратному контуру течет ток 4А, по круговому контуру 2А. Определить напряжённость магнитного поля в центре системы (в точке О)

Прямой бесконечный проводник имеет круговую петлю радиусом 8 см (рис. 7). Определить величину тока в проводнике, если известно, что магнитная индукция в точке А 1,25·10-4 Тл.

Напряженность магнитного поля в центре кругового контура с током 25 А/м, Радиус контура 10 см. Число завитков контура 5. Контур помещен в однородное магнитное поле с индукцией 10-5Тл. Магнитный момент контура составляет угол 30° с силовыми линиями магнитного поля.
Определить: магнитный момент контура; вращающий момент, действующий на контур; работу поворота контура из начального положения в положение, при котором а= 60 градусов.
Рамка длиной 4см и шириной 1,5см, содержащая 200 витков тонкой проволоки, находится в однородном магнитном поле с индукцией 0,1Тл. Плоскость рамки параллельна линиям индукции. По рамке течёт ток 1мА. Определить: магнитный момент рамки; вращающий момент, действующий на рамку; работу поворота рамки из начального положения в положение, при котором линии магнитной индукции перпендикулярны плоскости рамки.
Внутри длинного соленоида с плотностью витков n = 20см-1 расположен круговой контур радиуса R = 3см. Ток в витках соленоида I1 = 0,6А. Магнитный момент контура pm = 5,6·10-5А·м2. Нормаль к контуру составляет угол α = 60° с силовыми линиями поля соленоида. Определить: вращающий момент, действующий на контур; работу по удалению контура за пределы магнитного поля соленоида.
Длинный прямой провод и квадратный контур расположены так, как показано на рисунке. Магнитный момент контура 3∙10-2 Ам2, сила тока 6А, а = 10см. Определить работу по перемещению контура из положения, в котором l1 = 5см, в положение, в котором l2 = 10см.

Длинный прямой провод и прямоугольный контур расположены, как показано на рис. 9. I1 = 2 А; a = 5 см; b = 5 см; c = 5 см; I2 = 0.5 А. Определить работу по удалению контура в область пространства, где магнитное поле отсутствует.

Рамка площадью S = 200 см2 с числом витков N = 10 равномерно вращается с частотой n = 5 с-1 относительно оси, лежащей в плоскости рамки и перпендикулярной линиям индукции однородного магнитного поля (B = 0.2 Тл). Считая, что в начальный момент магнитный поток максимален, определить величину ЭДС в момент времени t = 0.25 с; количество электричества, которое индуктируется в рамке за промежуток времени от t1 = 0 до t2 = 0.3 с. Сопротивление рамки R = 2 Ом.
Квадратная рамка со стороной а = 8см и числом витков N = 5 находится в однородном магнитном поле, напряжённость которого меняется во времени по закону Н(t) =8·103 t2 А/м. Плоскость рамки перпендикулярна силовым линиям. Определить: эдс индукции в контуре в момент времени t = 3с; количество электричества, которое индуцируется в рамке за промежуток времени от t1 = 2с до t2 = 4с. Сопротивление рамки R = 2 Ом
Плотность витков бесконечно длинного соленоида 20 см-1. Ток в витках соленоида изменяется по закону. Внутри соленоида расположен круговой контур радиуса 5 см. Нормаль к контуру составляет угол 30° с силовыми линиями магнитного поля соленоида. Сопротивление контура 2 Ом. Определить: эдс индукции в момент времени t = 3 с; количество электричества, которое индуктируется в контуре за промежуток времени от t1 = 2 с до t2 = 4 с.
Бесконечно длинный прямой провод и прямоугольный контур расположены, как показано на рис.10. I = 3 A, a = 5 см, b = 10 см, с = 5 см. Сопротивление контура 3 Ом. В некоторый момент времени ток в проводе исчезает. Определить количество электричества, которое индуктируется в контуре. Покажите направление индукционного тока в контуре.

Бесконечно длинный прямой провод и квадратный контур расположены так, как показано на рисунке. Ток в проводе меняется во времени по закону. Сопротивление контура 3 Ом. Определить количество электричества, которое индуктируется в контуре за промежуток времени от t1 = 2с до t2 = 5с, a = 10 см; l = 5 см. Покажите направление индукционного тока в контуре.

Взаимная индуктивность двух контуров 0,05Гн. При изменении силы тока I1 в первом контуре во втором контуре возникает ток I2, который меняется по закону. Сопротивление контура 2 Ом. Определить: магнитный поток, сцепленный со вторым контуром, в момент времени t = 3с, считая, что в начальный момент времени этот поток равен нулю; величину тока в первом контуре в момент времени t = 3с.
Длинный прямой провод и прямоугольный контур расположены, как показано на рис. 12 а = 10 см, b = 20 см, c = 10 см. Определить взаимную индуктивность контура и провода.

Две катушки расположены на небольшом расстоянии друг от друга. Когда сила тока в первой катушке изменяется со скоростью dI1/dt = 5 А/с, во второй катушке возникает эдс индукции Е2 =0,1 В. Определить: коэффициент взаимной индукции катушек; магнитный поток сцепленный со второй катушкой, в момент времени t = 2 с, считая, что при t0 =0 ток в первой катушке I0 = 2 А.
Взаимная индуктивность двух контуров 0,05 Гн. В первом контуре ток изменяется во времени по закону I1 = 0.3t2 + 0.1t, А. Индуктивность первого контура 0,2 Гн. Определить: магнитный поток, сцепленный со вторым контуром, в момент времени t = 3 с; ЭДС самоиндукции в первом контуре в момент времени t = 3 с; количество электричество, которое индуктируется во втором контуре за промежуток времени от t1 = 3 с до t2 = 5 с. Сопротивление второго контура 5 Ом.
Длинный прямой соленоид из проволоки диаметром 0,5мм намотан так, что витки плотно прилегают друг к другу. Внутри соленоида расположен прямоугольный контур со сторонами 5 см и 8 см и с числом 5. Плоскость контура составляет угол 30° с осью соленоида. Определить взаимную индуктивность соленоида и контура.
Напряженность магнитного поля внутри длинного соленоида 6∙103)А/м. Длина соленоида 2 М, диаметр 4 см, число витков 6000. Определить: энергию магнитного поля соленоида; объемную плотность энергии.
Цепь состоит из катушки индуктивностью 1 Гн и сопротивлением 10 Ом и источника тока. Источник тока можно отключать, не разрывая цепи. Определить: время, по истечении которого сила тока уменьшается до 0,001 первоначального значения; энергию магнитного поля катушки в этот момент времени. Сила тока в цепи при подключении источника I0 = 2А.
Соленоид длиной 1м и диаметром 8см подключается к источнику с ЭДС 24В и внутренним сопротивлением 2 Ом. Соленоид изготовлен из медной проволоки (ρ = 1,95∙10-8 Ом∙м), витки которой плотно прилегают друг к другу. Диаметр проволоки 0,5мм. Определить: энергию магнитного поля соленоида через 0,001с после подключения источника; Объёмную плотность энергии в этот момент времени.
К источнику, ЭДС которого 19В, подключена катушка, сопротивление которой R1 = 5 Ом, а индуктивность 0,17Гн. Параллельно катушке подключено сопротивление R2 = 95 Ом. Определить силу тока через сопротивление R2 до размыкания цепи и спустя 0,001с после размыкания.
В замкнутом контуре ЭДС самоиндукции меняется во времени по закону εis = 0.4t (В). Индуктивность контура 0,2 Гн. Определить энергию магнитного поля контура в момент времени t = 2 с. В начальный момент времени сила тока в контуре I0 = 6 А.
Колебания точки массой 10 г заданы уравнение x = 5·10-2sin(0.5t), м. Определить: силу, действующую на точку в момент времени t = 2 с; полную энергию точки.
Точка массой 5 г совершает гармоническое колебание по закону x = 5sin(3πt/5 + π/3), см. Написать уравнения колебаний кинетической и потенциальной энергии точка; определить полную энергию точки.
Материальная точка массой 20 г совершает гармонические колебания. Максимальная скорость точки 0,1 м/с, амплитуда колебаний 4·10-2 м. В начальный момент времени смещение равно половине амплитуды. Написать уравнение колебаний. Определить силу, действующую на точку в момент времени t = Т/3.
Полная энергия колеблющегося тела 5·10-5 Дж, максимальная сила, действующая на тело, 2,5·10-3 Н, частота колебаний 0,5 Гц, начальная фаза 60°. Написать уравнение колебаний тела. Определить скорость и ускорение тела в момент времени t = T/6.
Точка совершает гармоническое колебание с циклической частотой 4,0 рад/с. В некоторый момент времени смещение точки от положения равновесия равно 0,25 м, скорость 1 м/с. Написать уравнение колебаний точки. Определить смещение и скорость точки в момент времени t = T/12. Начальную фазу принять равной нулю.
Уравнение колебания системы имеет вид
x=4·10-2·e-0.2t·sin(π/8·t) м
Определить: собственную частоту колебаний системы; амплитуду после трех полных колебаний.
Уравнение колебаний точки задано в виде: x = 5·10-2·e-0.25t·cos(πt/2), м. Определить логарифмический декремент затухания колебаний. За какой время амплитуда колебаний уменьшается в 10 раз?
Период затухающего колебания системы 2 с, логарифмический декремент 1,6; начальная фаза равна 0. В момент времени t = T/4 смещение равно 5 см. Написать уравнение колебаний. Определить число колебаний, по прошествии которых амплитуда убывает в 102 раз.
В начальный момент времени смещение колеблющейся точки максимально и равно 0,1 м. За 10 колебаний амплитуда уменьшается на 1/10 своей первоначальной величины. Период колебаний равен 0,4 с. Определить коэффициент затухания и логарифмический декремент колебаний. Написать уравнение колебаний.
Уравнение затухающих колебаний системы имеет вид x=10-1e-0.2tcosπ/8 м. Масса системы 0,1 кг. Определить: собственную частоту колебаний, коэффициент упругости, коэффициент сопротивления, логарифмический декремент затухания и амплитуду колебаний в момент времени 5 с.
Колебательный контур состоит из конденсатора емкостью 0,2 мкФ и катушки индуктивности 5 мГн. Максимальный заряд на конденсаторе равен 2·10-6 Кл. Написать законы изменения заряда на обкладках конденсатора и силы тока в контуре с течением времени. Определить энергию электрического поля и энергию магнитного поля в момент времени t = T/6.
Колебательный контур состоит из конденсатора ёмкостью 0,25 мкФ и катушки индуктивностью 0,5 Гн. Полная энергия контура 5·10-5Дж. Написать закон изменения с течением времени: силы тока в контуре; разности потенциалов на обкладках конденсатора. Считать, что в начальный момент времени заряд на конденсаторе максимальный.
В колебательном контуре разность потенциалов на обкладках конденсатора изменяется по закону: U=100sin(104t) В. Индуктивность контура 0,2 Гн. Определить емкость контура. Написать закон изменения с течением времени энергии электрического поля и энергии магнитного поля контура.
Частота колебаний в контуре 250 кГц. Индуктивность контура 1,0 мГн. Начальный заряд на конденсаторе максимален и равен 10-6 Кл. Определить емкость контура. Написать закон изменения с течением времени силы тока в контуре. Определить полную энергию контура. (Сопротивлением контура пренебречь).
Сила тока в колебательном контуре изменяется со временем по закону I = 2·10-2·sin(400πt), А. Индуктивность контура 1 Гн. Определить: период колебаний в контуре; емкость контура; энергию электрического и магнитного поля контура в момент времени t = T/4.
Колебательный контур состоит из катушки индуктивностью 0,2 мГн и двух конденсаторов емкостью 4 мкФ каждый. Максимальный тока в контуре 0,1 А. Определить: период собственных колебаний в контуре; максимальный заряд на конденсаторах и напряжение на каждом из них. Рассмотреть случаи последовательного и параллельного соединения конденсаторов.
Батарея, состоящая из двух конденсаторов емкостью 2 мкФ каждый, разряжается через катушку индуктивностью 1 мГн, сопротивление которой 50 Ом. Как нужно соединить конденсаторы (последовательно или параллельно), чтобы в контуре возникли колебания? Определить период колебаний. Написать закон изменения с течением времени разности потенциалов на батарее конденсаторов, считая начальный заряд 10-6 Кл равным максимальному.
Закон изменения во времени разности потенциалов на обкладках конденсатора в колебательном контуре задан в виде. Емкость конденсатора С = 10-6 Ф. Определить: индуктивность контура; максимальный заряд на конденсаторе и максимальную силу тока в контуре; полную энергию контура.
Колебательный контур состоит из конденсатора ёмкостью 7 мкФ, индуктивности 0,2Гн и сопротивления 20 Ом. Начальный заряд на конденсаторе 5·10-6Кл. Написать закон изменения со временем заряда на обкладках конденсатора. Определить период колебаний в контуре; логарифмический декремент затухания. Определить число колебаний, по прошествии которых амплитуда колебаний заряда уменьшается в 100 раз.
Точка участвует в двух одинаково направленных колебаниях одинаковых периодов 1,5 с. Амплитуды колебаний одинаковы и равны 2 см каждая. Начальные фазы колебаний равны π/2 и π/3. Написать уравнение результирующего колебания и построить векторную диаграмму.
Материальная точка массой 0,1кг участвует в двух одинаково направленных колебаниях, которые заданы уравнениями: x1=3cos(5t+0,2π) см; x2=5cos(5t+0,7π). Написать уравнение результирующего колебания. Определить полную энергию точки.
На горизонтально и вертикально отклоняющие пластины осциллографа подаются соответственно напряжения: Ux=10sin2t В, Uy=20sin(2t+φ) В. Написать уравнение траектории, описываемой электронным лучом на экране осциллографа, в двух случаях: φ=0; φ = π/2. Чувствительность пластин равны jx = jy = 2 мм/В.
Точка массой 2·10-2 кг участвует в двух одинаково направленных колебаниях одинаковых частот 2 Гц. Амплитуда первого колебания 5·10-2 м, начальная фаза π/6. Амплитуда второго колебания 7·10-2м, начальная фаза π/4. Определить: скорость точки в момент времени t = T/3; полную энергию колебаний.
На горизонтально и вертикально отклоняющиеся пластины осциллографа подаются соответственно напряжения: Ux = 20sin100πt, В, Uy = 25sin(100πt + π/6), В. Чувствительность пластин jx = jy = 2 мм/В.Написать уравнение траектории, описываемой электронным лучом на экране осциллографа. Найти время, через которое луч возвращается в исходную точку.
Вынужденные колебания описываются дифференциальным уравнением 0.4x + 0.48x + 1.6x = 0.8sin3t.

Определить: частоту вынужденных колебаний; частоту собственных колебаний системы; при какой частоте внешней силы будет наблюдаться резонанс.
Груз массой 2,5 кг, подвешенный к пружине с коэффициентом жесткости 3,6·102 Н/м, совершает вынужденные колебания под действием внешней силы F = 13.5sin6t, Н. Определить амплитуду вынужденных колебаний груза. Трением пренебречь.
Вынужденные колебания в электрическом контуре описываются дифференциальным уравнением q + 500q + 106q = 100sin103t.

Амплитуда ЭДС внешнего источника равна 4 В. Определить индуктивность, емкость и сопротивление контура, а также зависимость напряжения на обкладках конденсатора от времени.
В колебательный контур, состоящий из конденсатора ёмкостью 0,25 мкФ, катушки индуктивностью 0,01 Гн и сопротивления 100 Ом, включён генератор, создающий ЭДС. Написать дифференциальное уравнение вынужденных колебаний заряда контура. Найти зависимость силы тока в контуре от времени.
Уравнение собственных колебаний в электрическом контуре имеет вид U = Um·e-500t·sin1.41·103t, В. Найти зависимость напряжения на конденсаторе от времени при вынужденных колебаниях при включении в контур внешней ЭДС E = 1.6·sin103t, В.
Плоская волна, возбуждаемая вибратором, колеблющимся по закону x = 0,2sin20πt м, распространяется со скоростью 10 м/с. Написать уравнение плоской волны. Определить длину волны и период. Определить в момент t = 0,1 с смещение точки среды, находящейся на расстоянии 10,25 м от вибратора.
Источник колебаний с периодом 10-2с и амплитудой 5·10-4м посылает волну, распространяющуюся в среде со скоростью 300 м/с. Определить длину плоской волны. Написать уравнение волны. Определить максимальную колебательную скорость частиц среды.
В стальном стержне распространяется плоская продольная волна от источника, уравнение колебаний которого задано в виде: x = 10-5·sin102t, м. Модуль Юнга стали 2·1011 Н/м2; плотность стали 8·103 кг/м3. Написать уравнение волны. Определить: длину волны; максимальную относительную деформацию в стержне.
Уравнение незатухающих колебаний источника имеет вид: x=10-6sin102t м. Длина волны 15 м. Написать уравнение плоской волны. Определить: смещение точки среды, находящейся на расстоянии 20 м от источника в момент времени 0,01 с; разность фаз колебаний точек, расположенных на расстоянии 15 м и 20 м от источника.
Частота колебаний источника волн 300Гц. На расстоянии 0,3 м от источника волну можно считать сферической, амплитуда колебаний частиц воздуха на этом расстоянии 10-3мкм. Температура воздуха 17°С, плотность воздуха 1,2 кг/м3, молярная масса 29·10-3кг/моль. Написать уравнение волны, распространяющейся в воздухе. Определить плотность потока энергии на расстоянии 20 м от источника.
Уравнение плоской волны, распространяющейся в стержне сечением 10 см2, имеет вид: x = 6·10-6cos(1900t - 5.7z), м. Определить: частоту колебаний; длину волны; скорость распространения волны в стержне. Какую энергию переносит волна через сечение стержня за 2 с? Плотность материала стержня 4·103 кг/м3.
Плоская бегущая акустическая волна представлена уравнением x = 5·10-4sin(1980t – 6z), м. Определить: частоту колебаний; скорость и длину волны; максимальную относительную деформацию среды.
Уравнение сферической волны, распространяющейся в воздухе, имеет вид: x = 10-6/r sin(103t - 3r), м. Плотность воздуха 1,2 кг/м3. Определить: длину волны и ее скорость; максимальное акустическое давление и уровень сигнала на расстоянии 300 м от источника. Нулевая интенсивность равна 10-12 Вт/м2.
Звуковая волна прошла через перегородку, вследствие чего уровень сигнала уменьшился на 30 дБ. Во сколько раз уменьшилась интенсивность звука?
На расстоянии 10 м от источника звука, размеры которого малы, уровень сигнала равен 20 дБ. Пренебрегая затуханием, определить: уровень сигнала на расстоянии 5 м; на каком расстоянии звук не слышен. Нулевая интенсивность .
Уравнение сферической волны, распространяющейся в воздухе, имеет вид:
x=10-6/r·sin2π(103t-r/0.33) м.
Амплитуда акустического давления на расстоянии 10м от источника равна 0,2Па. Определить мощность источника звуковых волн и среднюю за период объёмную плотность энергии на расстоянии 100 м от источника. Определить уровень сигнала на этом расстоянии
Мощность точечного источника звуковых волн равна 25 Вт. Частота источника 1000 Гц. Температура воздуха 17°С, плотность воздуха 1,2 кг/м3, молярная масса 29 г/моль. Написать уравнение волны, распространяющейся в воздухе. Определить амплитуду акустического давления и уровень сигнала на расстоянии 10 м от источника.
В воздухе при температуре 17°С образуются стоячие волны. Расстояние между соседними пучностями 0,5 м. Определить частоту волны. Молярная масса воздуха 29·10-3 кг/моль
Уравнение стоячей волны в шнуре имеет вид x = 0.02sin2πz·sin200πt, м. Найти координаты узлов и пучностей, если длина шнура равна 1 м. Написать уравнения бегущих волн, из которых образована эта стоячая волна и определить их длину волны и скорость.
В струне массой 6 г и длиной 0,6 м образована стоячая волна. Сила натяжения струны равна 25 Н, амплитуда колебаний в пучности 0,5 см. Написать уравнение стоячей волны в струне, если она закреплена на концах и на ней имеются три пучности.
При приближении источника звука к наблюдателю кажущаяся частота равна 1100 Гц, при удалении 900 Гц. Определить скорость движения источника и частоту звука, издаваемого источником.
Два поезда идут навстречу друг другу со скоростями 72 км/час и 54 км/час. Первый поезд дает свисток с частотой 600 Гц. Определить частоту колебаний звука, который слышит пассажир второго поезда: перед встречей поездов; после встречи поездов. Скорость звука принять равной 340 м/с.
По озеру плывёт катер со скоростью 2м/с, а навстречу ему лодка со скоростью 1м/с. Скорость волн, создаваемых катером, относительно поверхности озера равна 3м/с, частота этих волн 0,5Гц. С какой частотой будет качаться лодка в волнах, создаваемых катером, до встречи с ним и после этой встречи.
С балкона вниз падает будильник, издающий звук, частота основного тона которого 1000 Гц. Найти закон изменения частоты основного тона, воспринимаемой стоящим внизу человеком. Температура окружающего воздуха t = 17 °C, молярная масса 29 г/моль, ускорение свободного падения 9,8 м/с2.
Движущийся со скоростью 108 кг/ч автомобиль подает звуковой сигнал частотой 600 Гц. С какой скоростью и в какую сторону движется второй автомобиль, если частота сигнала, воспринимаемого его водителем, равна 630 Гц. Температура воздуха 17°С, молярная масса 29 г/моль.
|  |  | Методичка 2001 часть 1 |  |
| |
Министерство Российской Федерации по связи и информатизации
Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича
Факультет вечернего и заочного обучения
Л.М.Черных, А.В.Кочерыженков
ФИЗИКА
ускоренное обучение
методические рекомендации и контрольные задания
Часть 1
Санкт-Петербург
2001
Стоимость решения одной задачи по физике уточняйте при заказе.
Выполнены следующие задачи:
Решенные задачи по физике
Задача 1
Тело массой 2кг движется под действием силы, меняющейся по закону F=12t.
Начальная скорость тела равна 2м/с. Найти: путь, пройденный телом за 4с
движения, начиная с t = 0, работу, совершённую силой за этот промежуток времени.
Задача 2
Импульс тела массой 0,5кг меняется согласно уравнению p=0.75t^3+2t . Найти путь, пройдены телом за промежуток времени от t1=2с до t2= 4с, величину силы, действовавшей на тело в момент времени t1.
Задача 3
Зависимость координаты тела от времени задана уравнением x=t^4+2t^2 . Кинетическая энергия тела от времени t1=1с равнялась 32Дж . Найти: работу силы, приложенной к телу, за промежуток от t1=1с до t2=2c ; величину этой силы в момент времени t2.
Задача 4
Кинетическая энергия тела растёт со временем по закону W=9t^4 Дж. Масса тела 2кг. Найти: путь, пройденный телом за промежуток времени от 1с до 3с; величину силы, приложенной к телу в момент времени t2.
Задача 5
Зависимость координаты тела от времени задана уравнением x = 24t - 2t(3)м. Масса тела 3кг. Найти работу силы, приложенной к телу, за промежуток времени от 0 до момента остановки; путь, пройденный телом за этот промежуток времени; величину силы, действующей на тело в момент остановки.
Задача 6
Вагон массой 20т, двигавшийся со скоростью 2м.с, сталкивается с вагоном массой 30т, двигавшимся со скоростью 1м.с в ту же сторону. Найти величину наибольшего сжатия буферов вагонов. В столкновении участвуют по два буфера каждого вагона. Коэффициент упругости каждого буфера принять равным 10^8 Н/м.Столкновение считать абсолютно упругим.
Задача 7
Два мальчика, стоящие на льду, оттолкнулись друг от друга. После толчка первый мальчик проехал до остановки расстояние 225м. Коэффициент трения коньков об лёд равен 2∙10-2. Масса первого мальчика 48кг, масса второго – 40кг. Найти работу совершённую мальчиками в процессе толчка
Задача 8
Два шара массами 2кг и 3кг висят на нитях длиной 0,5м и соприкасаются. Шары отвели в стороны от положения равновесия во взаимно перпендикулярных плоскостях на одинаковый угол 60 и одновременно отпустили. Скорости шаров при столкновении взаимно перпендикулярны. На какую высоту поднимутся шары после столкновения?
Задача 10
Два кубика, массы которых 0,3кг и 0,5кг, связаны короткой нитью. Между кубиками поместили пружину так, что она сжалась на 10см. Жёсткость пружины 192Н/м. Нить пережигают, и кубики приходят в движение. На какую высоту поднимется первый кубик по наклонной плоскости, находящейся на его пути? Основание наклонной плоскости перпендикулярно скорости этого кубика. Трением пренебречь.
Задача 11
На рисунке показаны заряженные плоскость MN ( σ = - 10-11Кл/см2) и шар (Q = 0,02мкКл); а = 10см. Найти: напряжённость электрического поля в точках А и С; работу сил поля при перемещении точечного заряда 01,нКл из точки А в точку С
Задача 12
На рисунке показаны заряженная нить τ1 = 0,2нКл/см и цилиндр τ2 = - 0,1нКл/см; а = 20см. Найти силы, действующие на частицу, заряд которой 0,1нКл, в точках А и С со стороны электрического поля; изменение потенциальной энергии частицы в электрическом поле при перемещении её из точки А в точку С.
Задача 13
На рисунке показаны заряженные нить MN(t=1нКл/см ) и шар (q=-0,08мкКл ),a=20см. Найти: угол между прямой OC и напряженностью электрического поля в точке C; силу, действующую со стороны электрического поля на точечный заряд q=-1нКл в этой точке; работу сил электрического поля по перемещению заряда q из точки А в точку С.
Задача 14
На рисунке показаны заряженные готовая нить и плоскость, а = 30 см. Найти: силу, действующую со стороны электрического поля на точечный заряд q0 = -1 нКл в точке А; изменение потенциальной энергии этого заряда в электрическом поле при перемещении его из точки А в точку С.
Задача 15
На рисунке показаны две заряженные плоскости: горизонтальная (σ1 = 2нКл/см2) и вертикальная (σ2 = -1нКл/см2); а = 30см. Найти: угол между прямой АО и напряжённостью электрического поля в точке А; силу, действующую со стороны электрического поля в точке А на точечный заряд q0 = – 0,3нКл; работу, которую необходимо совершить против сил электрического поля, чтобы переместить этот заряд из точки А в точку С.
Задача 16
Электрон, ускоренный разностью потенциалов 1000В, влетает посередине
между пластинами плоского конденсатора под углом 450 к оси параллельной пластинам. Длина пластин 10см, расстояние между ними 0,5см.
Какое напряжение надо подать на пластины, чтобы при вылете
из конденсатора смещение электрона поперек пластин отсутствовало?
Задача 17
Электрон, ускоренный разностью потенциалов 500В, влетает в плоский конденсатор параллельно его пластинам. Расстояние между пластинами 4мм, разность потенциалов между ними 10В. На выходе электрон смещается на 2мм в поперечном к пластинам направлении. Найти расстояние, пройденное электроном вдоль пластин; угол, на который он отклонится от первоначального направления.
Задача 18
Электрон, ускоренный разностью потенциалов U=200В , влетает в плоский конденсатор параллельно его пластинам. Длина пластин l=10см , расстояние между ними d=5см , разность потенциалов между пластинами U=100В . На каком минимальном расстоянии y от положительной пластины должен влететь электрон, чтобы он смог вылететь из конденсатора? Найти также угол а отклонения электрона от первоначального направления при вылете из конденсатора.
Задача 20
Электрон влетает между пластинами плоского конденсатора параллельно пластинам и на выходе из пластин оказывается смещённым на 2см от направления первоначального движения. Длина пластин 10см, расстояние между ними 5см, разность потенциалов между пластинами 20В. Найти скорость электрона на выходе из пластин.
Задача 21
Два параллельно соединённых плоских конденсатора, емкости которых
0,3нФ и 0,1 нФ, заряжены до разности потенциалов 100В и отключены
от источника. Расстояние между обкладками первого конденсатора (ε1 = 1) увеличивают в 3 раза. Найти энергию второго конденсатора
( d2 = 1см; ε2 = 10) после этой операции; объёмную плотность этой энергии.
Задача 22
Два параллельно соединённых конденсатора, емкости которых 50пФ и 150пФ, заряжены до разности потенциалов 50В и отключены от источника. После того как первый плоский конденсатор (d1 = 1мм) заполнили диэлектриком, разность потенциалов между обкладками конденсаторов стала равной 25В. Найти: энергию первого конденсатора после заполнения диэлектриком; объёмную плотность этой энергии.
Задача 23
Первый конденсатор, емкость которого С1=1мкФ, зарядили до разности потенциалов U1=5В, а второй, емкость которого U2=20В, до разности потенциалов. После этого конденсаторы отключили от источников и соединили между собой одноименно заряженными обкладками. Найти: количество теплоты, выделившееся при соединении конденсаторов; объемную плотность энергии электрического поля во втором плоском конденсаторе ( d2=5мкм,e2=10 ) после соединения конденсаторов.
Задача 24
Два параллельно соединенных плоских конденсатора, емкости которых С1=200пФ и С2=100пФ, зарядили, после чего источник отключили. Затем из первого конденсатора вынули диэлектрик (e2=4). В результате этого напряжение на конденсаторах стало равным 80 В. Найти: энергию второго конденсатора (d2=2мм, S2=100см^2) до вынимания диэлектрика из первого конденсатора, объемную плотность этой энергии.
Задача 25
Два параллельно соединённых плоских конденсатора зарядили от источника тока, после чего источник отключили. Затем расстояние между обкладками первого конденсатора, ёмкость которого была 300пФ, уменьшили в 2 раза. В результате этого энергия второго конденсатора (d2 = 4мм, ε2 = 2) стала равной 1,6∙10-7Дж, а её объёмная плотность 8,85∙10-4Дж/м3. Найти первоначальную разность потенциалов между обкладками конденсаторов
Задача 26
Напряжение на проводнике (n = 1022см-3, ρ = 10-4Ом•см; l = 5м;
S = 1мм2) изменяется согласно уравнению В. Найти: скорость
упорядоченного движения электронов в проводнике в момент времени
t1 = 1с; заряд, прошедший через поперечное сечение проводника
за промежуток времени от t1 = 1с до t2 = 3с; количество теплоты,
выделившееся в проводнике за тот же промежуток времени.
Задача 27
Зависимость от времени напряжённости поля в проводе (μ = 10см2/Вс; n = 2,2∙1022см-3;S = 1мм2) имеет вид В/м. Найти: заряд, прошедший через поперечное сечение провода за промежуток времени от t1 = 2с до t2 = 4с; количество теплоты, выделившееся в 10см3 провода за это время.
Задача 28
Плотность тока в проводе (n=2.2*10^23см^(-1) ,p=2.8*10^(-6)Ом*см ) описывается уравнением j=exp(-10*t)А/мм^2 . Найти: зависимость скорости упорядоченного движения электронов от времени; количество теплоты, выделившееся в 1см^3 провода за промежуток времени от t1=0 до t2=бесконечности .
Задача 29
Сила тока в проводе ( u = 35 см2 /В∙с,l = 40м, n = 1,02∙1023см-3,S = 0,1мм2 ) растёт в соответствии с выражением I = 0,1tA. Найти : число электронов, прошедших через поперечное сечение провода за промежуток времени от 1с до 4с; количество теплоты, выделившееся в проводе за это время.
Задача 30
Скорость упорядоченного движения электронов в проводе (u = 35 см2 /В∙с; n = 1,02∙1023см-3; S = 0,1мм2) задана уравнением . Найти : заряд, прошедший через поперечное сечение провода за промежуток времени от 3с до 5с; количество теплоты, выделившееся за это время в объёме 3см3 провода.
Задача 31
Электрон, ускоренный разностью потенциалов 4550 В, влетает в однородное магнитное поле под углом 30 к линиям магнитной индукции. Со стороны поля на электрон действует сила 9,1*10(-15)Н. Найти: период обращения электрона, радиус и шаг винтовой траектории.
Задача 32
Электрон, ускоренный разностью потенциалов 100В, влетает в однородное магнитное поле под углом 300 к линиям магнитной индукции. Сделав 5 оборотов по винтовой линии, он пролетает область поля длиной 10см. Найти радиус и шаг винтовой траектории, а также индукцию магнитного поля.
Задача 33
Протон (ь=1,67*10^(-27) ,q=1.6*10^(-19) ) движется в однородном магнитном поле по винтовой линии, шаг которой равен 5мм , а радиус 1мм . Индукция поля В=0,1Тл. Найти: скорость протона и угол между скоростью протона и индукцией магнитного поля.
Задача 34
В однородном магнитном поле, индукция которого В = 0,01 Тл, движутся по окружности со скоростью 10(7) м/с один за другим 100 электронов. Найти эквивалентную силу тока и магнитный момент кругового контура, образованного этим движением.
Задача 35
Электрон влетает в однородное магнитное поле под углом 300 к линиям магнитной индукции. Сделав 10 оборотов по винтовой линии, он пролетает область поля длиной 15см за 30нс. Найти: силу, действовавшую на электрон со стороны магнитного поля, и разность потенциалов электрического поля, которой он был ускорен перед попаданием в магнитное поле.
Задача 36
Магнитное поле создаётся двумя параллельными длинными проводами, по которым текут токи 3А и 4А. а = 10см. Найти индукцию магнитного поля в точке О; угол между вектором магнитной индукции в точке О и прямой ОА.
Задача 37
Магнитное поле создаётся прямым длинным проводом с током 3А и круговым контуром радиусом 10см, имеющим 10 витков; а = 20см. Найти ток в контуре, если индукция результирующего магнитного поля в центре контура 5∙10-6Тл
Задача 38
Магнитное поле создается соленоидом с током и прямым длинным проводом с током I2=3А, а=30см. Радиус соленоида R=10см, число витков, приходящихся на единицу длины n=1000м^(-1). Найти отношение магнитных индукций в точках А и С, прилегающих к виткам соленоида, соответственно, с внутренней и внешней стороны.
Задача 39
В центре соленоида с током 50 мА находится круглый контур, по которому течет ток = 100 мА. Длина соленоида 50 см, число витков = 1000. Число витков контура = 20, его радиус = 1 см, плоскость витков контура параллельна оси соленоида. Под каким углом к оси соленоида направлена индукция магнитного поля в центре контура? Найти величину этой индукции.
Задача 40
Магнитное поле создаётся соленоидом с током 100мА и прямым длинным проводом с током 50А, находящимся на расстоянии 30см от оси соленоида и перпендикулярным этой оси. Радиус соленоида 20см, плотность намотки 5см-1. На каком расстоянии от оси соленоида находится ближайшая точка, в которой магнитная индукция равна нулю?
Задача 41
Маленькая рамка площадью 2см2, имеющая 200 витков и сопротивление
1 Ом, находится на расстоянии 1м от длинного прямого провода с
переменным током А. Магнитное поле провода в пределах рамки можно
считать однородным. Найти: взаимную индуктивность рамки и провода;
максимальное значение тока в рамке; заряд, прошедший в рамке при
изменении тока в проводе от максимального значения до нуля.
Задача 42
Внутри соленоида с током 2А и плотностью намотки 5см-1 вращается с частотой 10 об/с рамка, площадь которой 10см2, число витков 100, сопротивление 5 Ом. Ось вращения перпендикулярна линиям индукции магнитного поля соленоида. Найти: максимальную и минимальную взаимные индуктивности рамки и соленоида; зависимость от времени индукционного тока в рамке.
Задача 43
Индуктивность первого контура L=0.1Гн, его потокосцепление изменяется вследствие изменения тока этого контура согласно уравнению 0.2t^2 Вб. Взаимная индуктивность первого и второго контуров М=0,001Гн . Сопротивление второго контура R2=2 Ом. Найти: ток во втором контуре, вызванный явлением взаимной индукции, в момент времени t1=1c ; заряд, прошедший по цепи второго контура за промежуток времени от t1=1c до t2=3c.
Задача 44
Площадь квадратной рамки = 0,25 м2, число витков = 100, диаметр медного провода = 1 мм. С какой частотой надо вращать эту рамку вокруг оси, перпендикулярно линиям напряженности магнитного поля Земли, чтобы эффективное значение тока в ней было равно 1 мА?
Задача 45
Зависимость от времени индукции однородного магнитного поля имеет вид. В этом поле расположен контур так, что нормаль к его плоскости составляет угол 600с линиями магнитной индукции. Площадь контура 0,5м2, число витков 500, сопротивление 50 Ом. Найти: силу тока в контуре в момент времени 2с, заряд, прошедший по цепи контура за промежуток времени от 2с до 4с.
Задача 46
На цилиндрический деревянный сердечник длиной 0,5м и
диаметром 10см плотно намотали провод диаметром 1мм.
Полученный соленоид, сопротивление которого оказалось
равным 7 Ом, подключили к источнику тока с ЭДС 14В.
Затем на такой же сердечник на всю его длину плотно намотали
провод диаметром 0,5мм с тем же удельным сопротивлением и
подключили к такому же источнику тока, как и в первом случае.
Найти: энергию магнитного поля и объёмную плотность
этой энергии в первом и втором случаях. Сопротивления
источников считать равными нулю.
Задача 47
Вдоль оси соленоида с током 0,2А проходит провод с током 12,56А. Длина соленоида 1м, число витков 1000, площадь витка 10см2. Найти энергию магнитного поля соленоида; объёмную плотность энергии результирующего магнитного поля на расстоянии 1см от провода
Задача 48
Длина соленоида l=1м, диаметр D=10см. На соленоид плотно намотан провод диаметром d=1мм . Какой ток надо пропустить по соленоиду, чтобы энергия его магнитного поля была равна энергии магнитного поля Земли, заключенной в комнате размером 8*4*2,5м^3 ? Найти отношение объемных плотностей энергии магнитного поля соленоида и Земли. Напряженность магнитного поля Земли принять равной H0=40 А/м.
Задача 49
Ток в соленоиде меняется согласно уравнению I=4*e^(-500). Длина соленоида I=0.5м, площадь одного витка S=100см^2, число витков N=1000 . Найти: время, за которое энергия магнитного поля соленоида уменьшается в 10 раз; значение этой энергии и ее объемной плотности по истечении этого промежутка времени (время отсчитывать от момента t=0 ).
Задача 50
Два соленоида имеют одинаковую плотность витков, намотанных из одинакового провода. Площади поперечного сечения соленоидов одинаковы, но первый соленоид вдвое короче второго. Соленоиды соединили параллельно друг другу и подключили к источнику тока. Во сколько раз отличаются энергии магнитного поля соленоидов и объёмные плотности энергии
Дата выполнения: 19/11/06
|  |  | Методичка 2002 часть 2 |  |
| |
Министерство Российской Федерации по связи и информатизации
Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича
Факультет вечернего и заочного обучения
Л.М.Черных, А.В.Кочерыженков
ФИЗИКА
ускоренное обучение
методические рекомендации и контрольные задания
часть 2
Санкт-Петербург
2002
Стоимость решения одной задачи по физике уточняйте при заказе.
Готовы следующие задачи:
Решенные задачи по физике
Задача 1.
Зависимость напряжения на обкладках конденсатора от времени при свободных колебаниях в колебательном контуре имеет вид U=20sin{105+π/4}B. Индуктивность контура L=0,1мГн.
Найти зависимость силы тока в контуре от времени. Начертить графики зависимости от времени энергии электрического поля конденсатора, энергии магнитного поля катушки и полной энергии в пределах одного периода.
Дано: U=20sin{105+π/4}B,L=0,1мГн=1·10-4Гн.
Найти: I(t), Wэ(t), Wм(t), W(t).
Задача 2.
Зависимость силы тока в контуре от времени при свободных колебаниях в имеет вид I=3,14·10-2cos{5·104πt-π/4}A. Емкость конденсатора контура С=0,1мкФ.
Найти зависимость напряжения на конденсаторе от времени. Начертить графики зависимости от времени в пределах одного периода энергии электрического поля, энергии магнитного поля и полной энергии контура.
Дано:
Найти:
Задача 3.
Энергия колебательного контура W=2мкДж, его индуктивность L=0.04мГн. Напряжение на конденсаторе в начальный момент времени равно максимальному значению Um=0.4В. Найти зависимость заряда конденсатора от времени в режиме свободных колебаний. Начертить графики зависимости от времени в пределах одного периода энергий электрического и магнитного полей, а также полной энергии контура. Затуханием пренебречь.
Дано:
Найти:
Задача 4.
Луч естественного света падает под углом Брюстера aБ на
поверхность диэлектрика.Отраженный луч, интенсивность которого I1=0,4Вт/см2, проходит через поляризатор P. При этом его интенсивность уменьшится до значения I2=0,3 Вт/см2. Найти угол φ между плоскостью падения луча на диэлектрик и плоскостью поляризации луча (плоскостью, содержащей луч и направление колебаний вектора напряженности электрического поля E), вышедшего из поляризатора. Потерями в поляризаторе пренебречь.
Дано:
Найти:
Задача 5.
Индуктивность катушки контура L=0.4мГн, емкость его конденсатора C=1мкФ. В контуре происходят свободные колебания. Заряд конденсатора в начальный момент времени t=0 находился в стадии нарастания и равнялся половине амплитудного значения. В некоторый момент времени t заряд на конденсаторе и сила тока в контуре равны соответственно q(t0)=0.2мкКл, I(t0)=20мА. Пренебрегая затуханием, найти зависимость от времени энергий электрического и магнитного полей контура.
Дано:
Найти:
Задача 6.
6. Колебания, совершаемые частицами воздуха в точке наблюдения при прохождении звуковых волн, излучаемых первым и вторым источниками, описываются уравнениями: x1=sin103πtМКМ, x2=2sin[103πt+(2/3)π]МКМ.
Написать уравнение результирующего колебания, если через точку наблюдения обе волны проходят в одном направлении. Построить векторную диаграмму складываемых колебаний.
Дано:
Найти:
Задача 7.
Уравнения колебаний токов, втекающих в узел электрической схемы (рис.7), имеют вид: I1=8sin(800πt+π)мА, I2=6sin(800πt+3π/4)мА. Написать уравнение колебаний тока I , вытекающего из этого узла. Построить векторную диаграмму складываемых колебаний.
Дано:
Найти:
Задача 8.
В точку наблюдения приходят сигналы от двух антенн так, что напряженности полей имеют вид: Е1=40sin(106πt+π/6)мкВ/м, Е2=30sin(106πt+π/2)мкВ/м. Найти зависимость от времени напряженности поля результирующего сигнала, если оба вектора Е1 и Е2 совершают колебания вдоль одного направления. Построить векторную диаграмму складываемых колебаний.
Дано:
Найти:
Задача 9.
Два электромагнита создают магнитные поля, магнитные индукции которых описываются уравнениями:B1=0.1cos100пиf Тл, B2=0.05cos(100пиf+пи/4) Тл.
Имеются две одинаковые рамки (рис.8) каждая площадью S=100 см2. Плоскости рамок перпендикулярны линиям индукции магнитных полей. Найти зависимость от времени ЭДС в цепи, в которую эти рамки включены последовательно. Построить векторную диаграмму складываемых ЭДС.
Задача 10.
При прохождении через точку наблюдения одной продольной волны колебательная скорость частиц среды изменяется по закону x1=3sin(10^4t+пи/2) см/с. При прохождении через эту точку другой продольной волны колебательная скорость изменяется по закону x1=5sin(10^4t+пи/4) см/с. Найти закон изменения колебательной скорости x(t) в точке наблюдения, если через нее распространяются одновременно обе продольные волны в одном направлении. Построить векторную диаграмму.
Задача 11.
Уравнение плоской звуковой волны имеет вид x(t, z)=10-3sin200π(t-z/330)мм. Плотность воздуха p=1.3кг/м3. Найти период колебаний, длину волны, среднюю за период плотность звуковой энергии и уровень интенсивности. Определить энергию, переносимою волной через площадку S=1м2 за время t=1мин.
Дано:
Найти:
Задача 12.
Плоская гармоническая звуковая волна распространяется в воздухе. Плотность воздуха р=1,3кг/м3 , атмосферное давление р=105Па. Энергия, переносимая на время t=1 мин через площадку S=0.6м2, перпендикулярную направлению распространения волны, равна W=0.36мДж. Разность фаз колебаний между двумя точками Δφ= π/5рад, расстояние между этими точками Δz=0.25м. Написать уравнение волны. Определить амплитуду акустического давления и уровень интенсивности волны.
Дано:
Найти:
Задача 13.
Уравнение сферической волны, распространяющейся в воздухе, имеет вид x(t,r)=10-5 /r·sin(103t-3r)м. Плотность воздуха р=1,3кг/м3. Найти мощность источника волны, а также среднюю за период плотность звуковой энергии и уровень интенсивности сигнала на расстоянии r1=100м от источника.
Дано:
Найти:
Задача 14.
Частота колебаний источника гармонической сферической звуковой волны v=500Гц. Плотность воздуха р=1.3кг/м3, атмосферное давление р=105Па. Через площадку S=100см2 за время Δt=1мин волна переносит энергию W=0.6мДж. Площадка перпендикулярна направлению распространению волны и находится на расстоянии r1=50м от источника. Найти уровень интенсивности сигнала в пределах площадки. Написать уравнение волны. Определить мощность источника волны.
Дано:
Найти:
Задача 15.
Частота источника гармонической сферической звуковой волны v=1000 Гц. Плотность воздуха p=1.3 кг/м3, его температура T=290 К, масса моля М=29 г/моль. На расстоянии r1=100 м от источника уровень интенсивности волны L=80 дБ. Написать уравнение волны. На каком расстоянии от источника уровень интенсивности звука достигнет порога болевого ощущения Lп=120 дБ?
Задача 16.
Луч плоскополяризованного света последовательно проходит через 2 поляризатора. Плоскость пропускания 2-го поляризатора перпендикулярна плоскости поляризации луча, падающего на 1-й поляризатор. При каком угле α между плоскостью пропускания 1-го поляризатора и плоскостью поляризации падающего на него света интенсивность I2 света, прошедшего оба поляризатора, будет максимальна? Найти интенсивность, если начальная интенсивность луча I0=0.1Вт/см2?
Дано:
Найти:
Задача 17.
На поляризатор падает плоскополяризованный луч света. После прохождения поляризатора интенсивность света уменьшается в 4 раза. На какой угол надо повернуть плоскость пропускания поляризатора, чтобы он полностью гасил проходящий свет? Потери в поляризаторе не учитывать.
Дано: I0/I1=4
Найти:α.
Задача 18.
Естественный свет падает на систему из двух поляризаторов–николей, угол между плоскостями пропускания которых a=60о . При прохождении естественного света через поляризатор–николь его интенсивность уменьшается в 2 раза. После поворота плоскости пропускания одного из поляризаторов интенсивность луча, прошедшего систему, стала равна I2=0.2Вт/см2, увеличившись в 2 раза. Найти интенсивность луча естественного света и угол между плоскостями поляризаторов после поворота. Потерями в поляризаторах пренебречь.
Задача 19.
Луч естественного света, распространяющегося в горизонтальной плоскости,
падает под углом Брюстера на вертикальную поверхность диэлектрика.
Отраженный от диэлектрика луч проходит через поляризатор. в результате чего
его интенсивность уменьшается в 4 раза. найти угол между горизонтальной плоскостью и плоскости поляризации луча, вышедшего из поляризатора. Потерями в поляризаторе пренебречь.
Дано:
Найти:
Задача 20.
Плоскости поляризации двух параллельных пучков света взаимно перпендикулярны, а интенсивности одинаковы и равны I1=I2=0.5Вт/с2. На их пути ставят поляризатор. Доказать, что после прохождения поляризатора сумма интенсивностей этих пучков не зависит от ориентации плоскости пропускания поляризатора. Определить сумму интенсивностей прошедших пучков. Потерями в поляризаторе пренебречь.
Дано:I1=I2=0.5Вт/с2
Найти:I3+I4.
Задача 21.
Свет с длиной волны λ=4500Å от двух когерентных источников S1 и S2 попадает на экран Э, расположенный на расстоянии l=1.5 м (рис.4). На отрезке экрана a=3мм помещаются 3 интерференционные полосы. Наблюдатель способен различить не более 6 полос на указанном отрезке. На какую максимальную величину Δd можно увеличить расстояние между источниками, чтобы наблюдатель еще мог различать интерференционные полосы?
Дано:
Найти:
Задача 22.
Параллельный пучок лучей с длиной волны λ=6000Å падает на пленку толщиной d=0.25мкм, имеющую показатель преломления n=1.4 . При каком угле падения a отраженный свет будет максимально ослаблен в результате интерференции? Образование интерферирующих лучей показать на рисунке.
Дано:
Найти:
Задача 23.
Интерференция от 2-х когерентных источников (щелей) S1 и S2 наблюдается на экране Э, параллельном источникам (рис.4). Расстояние от экрана до источников 2м, длина волны света λ=4500Å. 5-й интерференционный максимум находится на расстоянии x=3мм от центра экрана О. Найти расстояние d между источниками. На какое расстояние Δl надо отодвинуть экран, чтобы ширина интерференционной полосы увеличилась в 1,5 раза?
Дано:
Найти:
Задача 24.
На мыльную пленку толщиной d=0.15мкм падают параллельные лучи с длиной волны λ=4500Å под углом a=45о. Найти показатель преломления мыльной пленки, если отраженные лучи при интерференции максимально усилены. При расчетах учесть, что показатель преломления мыльной пленки находится в интервале 1<n<2 . Образование интерферирующих лучей показать на рисунке.
Дано:
Найти:
Задача 25.
Два когерентных источника(щели) S1 и S2 находятся на расстоянии d=1мм друг от друга. Интерференция наблюдается на экране Э, расположенном на расстоянии l=2м от щелей(рис.4). Ширина интерференционной полосы на экране 1,2мм.
Задача 26.
Источник сферической волны S и точка наблюдении А находятся на оси круглого отверстия на расстояниях a и b от него (рис.5). Радиус отверстия r . Изменится или нет интенсивность света в точке наблюдения, если источник и точку наблюдения поменять местами?. Как изменится интенсивность в точке наблюдения в следующих случаях: 1) расстояния a от отверстия до источника и b от отверстия до точки наблюдения одновременно увеличивают в 2 раза ( до увеличения в отверстии укладывалось 6 зон Френеля); 2) радиус отверстия, в котором укладываются 4 зоны Френеля, уменьшают в 2 раза; 3) длину волны уменьшают в 2 раза (до уменьшения в отверстии укладывалась 1 зона Френеля). Ответы обосновать.
Дано:
Найти:
Задача 27.
Монохроматическая световая волна (λ=5000Å) излучается точечным источником S , расположенным на оси круглого отверстия (рис.5). Расстояние от источника до отверстия a=1м, радиус отверстия r=1мм. В отверстии укладываются 3 зоны Френеля. На каком расстоянии b от отверстия находится точка наблюдения А? Минимум или максимум наблюдается в точке А?
Дано:
Найти:
Задача 28.
Точечный источник света S и точка наблюдения А находятся на расстояниях, соответственно, a=1м и b=2м от него (рис.5). Длина волны λ=10-7м. При каком минимальном радиусе r отверстия в точке наблюдения будет иметь место максимум интенсивности?
Дано:
Найти:
Задача 29.
Источник света S находится на оси круглого отверстия на расстоянии a=1,25 м от него (рис. 5). Спектр источника содержит две длины волны λ1=4000Å (фиолетовый цвет) и λ2=6000Å (желтый цвет). какой цвет увидит наблюдатель в точке А, находящийся на расстоянии b=2,5 м от отверстия? Радиус отверстия r=1 мм.
Дано:
Найти:
Задача 30.
На круглое отверстие падает монохроматическая волна ( λ=0,72мкм). Радиус отверстия r=1.2мм. Точка наблюдения А находится на оси отверстия на расстоянии b=2м от него (рис.5). В отверстие укладывается 2 зоны Френеля. На каком расстоянии a от отверстия находится источник? Минимум или максимум интенсивности наблюдается в точке А?
Дано:
Найти:
Задача 31.
С поверхности серого тела площадью S=10см2 за 1 мин. излучается энергия W=34.02кДж. Коэффициент поглощения тела a=0.625. Найти температуру тела и длину волны, на которую приходится максимум излучательной способности этого тела.
Дано:
Найти:
Задача 32.
Абсолютно черное тело, имеющее температуру t1=727С, излучает с площади S1=20см2 за промежуток времени Δt1=5мин. такую же энергию, какую излучает второе абсолютно черное тело с площади S2=10см2 за промежуток времени Δt2=2.5мин. Определить длину волны λ, при которой излучательная способность второго тела максимальна?
Дано:
Найти:
Задача 33.
Абсолютно черное тело нагрето до температуру t=1727оС. Найти длину волны, на которую приходится максимум излучательной способности этого тела. На какой из двух длин волн λ1=5000Å или λ2=1000Å излучательная способность этого тела больше (ответ обосновать)?. Какую энергию излучает это тело за 1 час, если площадь его поверхности S=50см2?
Дано:
Найти:
Задача 34.
Абсолютно черное тело в виде шара радиусом r1=1 см излучает за промежуток времени t1=10 мин. энергию W1=684 кДж. Оно находится внутри сферической полости радиусом r2=10 см, стенки которой также излучают как абсолютно черное тело. Шар и полость и полость находятся в состоянии термодинамического равновесия. Найти: энергию , излучаемую стенками полости за промежуток времени t2=1 мин; длину волны , на которую приходится максимум излучательной способности полости.
Задача 35.
Какую энергию излучает за промежуток времени t=10мин с поверхности S=100см^2 серое тело, коэффициент поглощения которого a=0.5, если максимум излучательной способности этого тела приходится на длину волны 2,9*10^(-4).
Задача 36.
Изменение в 1,5 раза частоты ультрафиолетового излучения, падающего на вещество с работой выхода A=4эВ, привело к увеличению задерживающей разности потенциалов в 2 раза. Найти энергию и импульс фотонов, падающих на вещество до изменения частоты света.
Дано:
Найти:
Задача 37.
Ультрафиолетовое излучение, длина волны которого λ1=2,3·10-7м, падает на вещество и вызывает фотоэффект. При облучении второго вещества задерживающая разность потенциалов остается такой же, что и для первого вещества, если увеличить частоту излучения на величину Δv=2·1014Гц. Длины волн, соответствующие красным границам этих веществ, отличаются в 1,25 раза. Найти максимальные энергию и скорость фотоэлектронов, выбиваемых из первого вещества.
Дано:
Найти:
Задача 38.
Максимальная скорость электронов, вылетающих из вещества при фотоэффекте, Vm=8.4·105м/с. При увеличении энергии падающих фотонов в 2 раза максимальная скорость фотоэлектронов изменилась в 2 раза. Найти длину волны излучения, первоначально падавшего на вещество, и работу выхода для данного вещества.
Дано:
Найти:
Задача 39.
При падении ультрафиолетового излучения на одно вещество максимальная скорость выбиваемых фотоэлектронов Vm=7·105м/с. При падении этого излучения на другое вещество энергия выбиваемых фотоэлектронов изменилась в 1,5 раза. Работа выхода электронов из второго вещества составляет 84,5% от работы выхода из первого вещества. Найти частоту и импульс падающих фотонов.
Дано:
Найти:
Задача 40.
На вещество падает электромагнитное излучение, частота которого в 1,5 раза превышает частоту, соответствующую красной границе фотоэффекта для этого вещества. При этом задерживающая разность потенциалов Uз=1,25 В. Найти работу выхода электронов из вещества и импульс падающих фотонов.
Задача 41.
Кинетическая энергия электрона, выбитого фотоном из атома водорода, оказалась равна по модулю полной энергии этого электрона, которую он имел в атоме водорода. Найти энергию фотона, выбившего этот электрон. Длина волны де Бройля выбитого электрона λБ=6,645 Å.
Дано:
Найти:
Задача 42.
Электрон, находящийся на некотором энергетическом уровне в атоме водорода, может перейти в основное состояние одним из 4 различных способов через ниженаходящиеся энергетические уровни. Найти длину волны де Бройля электрона на исходном уровне и суммарную энергию фотонов, испущенных при таком переходе. Показать вышеупомянутые 4 перехода на энергетической диаграмме водорода.
Найти:λБ, ε.
Задача 43.
Энергия электрона, перешедшего с одного энергетического уровня на другой в атоме водорода, изменилась в 4 раза, а энергия испущенного при этом переходе фотона оказалась равна ε=4,1·10-19Дж. Найти номера начального и конечного энергетических уровней и длину волны де Бройля электрона в конечном состоянии.
Дано:
Найти:
Задача 44.
Найти отношение длины боровской орбиты в атоме водорода к длине волны де Бройля электрона, движущегося по этой орбите. Указать численные значения этого отношения для 1-й и 3-й орбит.
Дано:
Найти:
Задача 45.
Чему должна быть равна максимальная длина волны де Бройля электрона, чтобы при соударении он мог ионизировать атом водорода, находящийся в основном состоянии?
Найти:λБ
Дата выполнения: 05/05/2009
|  |  | Методичка 2012 спец главы |  |
| |
Федеральное агентство связи
Государственное образовательное учреждение
высшего профессионального образования
Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича
Факультет заочного обучения
Ускоренное обучение
Л.М. Черных, А.В. Кочерыженков
ФИЗИКА (СПЕЦ. ГЛАВЫ)
Методические рекомендации и контрольные задания
Санкт-Петербург
2012
Стоимость решения одной задачи по физике уточняйте при заказе.
Готовы следующие задачи:
Решенные задачи по физике
Задача 1.
Зависимость напряжения на обкладках конденсатора от времени при свободных колебаниях в колебательном контуре имеет вид. Индуктивность катушки контура L = 0,1мГн Найти зависимость силы тока в контуре от времени. Начертить графики зависимости от времени энергии электрического поля конденсатора, энергии магнитного поля катушки и полной энергии в пределах одного периода.
Задача 2.
Зависимость силы тока в контуре от времени при свободных колебаниях имеет вид. Емкость конденсатора контура. Найти зависимость напряжения на конденсаторе от времени. Начертить графики зависимости от времени в пределах одного периода энергии электрического поля, энергии магнитного поля и полной энергии контура.
Задача 4.
В контуре происходят свободные гармонические колебания. В начальный момент времени напряжение на конденсаторе находилось в стадии нарастания и равнялось В, что составляло половину амплитудного значения. Амплитуда силы тока в контуре, индуктивность контура. Пренебрегая затуханием, найти зависимость от времени энергий электрического и магнитного полей контура, а также полную энергию контура.
4. В контуре происходят свободные гармонические колебания. В начальный момент времени напряжение на конденсаторе находилось в стадии нарастания и равнялось 5В, что составило половину амплитудного значения. Амплитуда силы тока в контуре 0,1А, индуктивность контура 0,01мГн. Пренебрегая затуханием, найти зависимость от времени энергий электрического и магнитного полей контура, а также полную энергию контура.
Задача 6.
Колебания, совершаемые частицами воздуха в точке наблюдения при прохождении звуковых волн, излучаемых первым и вторым источниками, описываются уравнениями.
Написать уравнение результирующего колебания, если через точку наблюдения обе волны проходят в одном направлении. Построить векторную диаграмму складываемых колебаний.
Задача 7.
Уравнения колебаний токов, втекающих в узел электрической схемы, имеют вид. Написать уравнение колебаний тока, вытекающего из этого узла. Построить векторную диаграмму складываемых колебаний.
Задача 10.
При прохождении через точку наблюдения одной продольной волны колебательная скорость частиц среды изменяется по закону. При прохождении через эту точку другой продольной волны колебательная скорость изменяется по закону см/с. Найти закон изменения колебательной скорости в точке наблюдения, если через нее распространяются одновременно обе продольные волны в одном направлении. Построить векторную диаграмму складываемых скоростей.
Задача 11.
Уравнение плоской звуковой волны имеет вид. Плотность воздуха 1,3 кг/м3. Найти период колебаний, длину волны, среднюю за период плотность звуковой энергии и уровень интенсивности. Определить энергию, переносимую волной через площадку 1 м2 за время 1 мин.
Задача 12.
Плоская гармоническая звуковая волна распространяется в воздухе. Плотность воздуха 1,3 кг/м3, атмосферное давление 10(5) Па. Энергия, переносимая за время 1 мин. через площадку 0,6 м2, перпендикулярную направлению распространения волны, равна 0,36 мДж. Разность фаз колебаний между двумя точками, расстояние между этими точками 0,25 м. Написать уравнение волны. Определить амплитуду акустического давления и уровень интенсивности волны.
Задача 16.
Луч плоскополяризованного света последовательно проходит через 2 поляризатора. Плоскость пропускания 2-го поляризатора перпендикулярна плоскости поляризации луча, падающего на 1-й поляризатор. При каком угле α между плоскостью пропускания 1-го поляризатора и плоскостью поляризации падающего на него света интенсивность I2 света, прошедшего оба поляризатора, будет максимальна? Найти эту интенсивность, если начальная интенсивность луча I0 = 0,1 Вт/см2.
Задача 17.
На поляризатор падает плоскополяризованный луч света. После прохождения поляризатора интенсивность света уменьшается в 4 раза. На какой угол надо повернуть плоскость пропускания поляризатора, чтобы он полностью гасил проходящий свет? Потери в поляризаторе не учитывать.
Задача 21.
Свет с длиной волны 4500 Å от двух когерентных источников S1 и S2 попадает на экран Э, расположенный на расстоянии 1,5м. На отрезке экрана а = 3 мм помещаются 3 интерференционные полосы. Наблюдатель способен различить не более 6 полос на указанном отрезке. На какую максимальную величину можно увеличить расстояние между источниками, чтобы наблюдатель еще мог различать интерференционные полосы?
Задача 22.
Параллельный пучок лучей с длиной волны 6000 Å падает на пленку толщиной 0,25 мкм, имеющую показатель преломления 1,4. При каком угле падения отраженный свет будет максимально ослаблен в результате интерференции? Образование интерферирующих лучей показать на рисунке.
Задача 23.
Интерференция от 2-х когерентных источников (щелей) S1 и S2 наблюдается на экране Э, параллельном источникам (рис.4). Расстояние от экрана до источников 2 м, длина волны света 4500 Å. 5-й интерференционный максимум находится на расстоянии 3 мм от центра экрана О. Найти расстояние d между источниками. На какое расстояние ΔL надо отодвинуть экран, чтобы ширина интерференционной полосы увеличилась в 1,5 раза?
Задача 26.
Источник сферической волны S и точка наблюдения А находятся на оси круглого отверстия на расстояниях a и b от него. Радиус отверстия r. Изменится или нет интенсивность света в точке наблюдения, если источник и точку наблюдения поменяли местами? Как изменится интенсивность в точке наблюдения в следующих случаях: 1) расстояния a от отверстия до источника и b от отверстия до точки наблюдения одновременно увеличивают в 2 раза (до увеличения в отверстии укладывалось 6 зон Френеля); 2) радиус отверстия, в котором укладываются 4 зоны Френеля, уменьшают в 2 раза; 3) длину волны уменьшают в 2 раза (до уменьшения в отверстии укладывалась 1 зона Френеля). Ответы обосновать.
Задача 27.
Монохроматическая световая волна (5000 Å) излучается точечным источником S, расположенным на оси круглого отверстия. Расстояние от источника до отверстия а = 1 м, радиус отверстия 1 мм. В отверстии укладываются 3 зоны Френеля. На каком расстоянии от отверстия находится точка наблюдения А? Минимум или максимум интенсивности наблюдается в точке А?
Задача 29.
Источник света находится на оси круглого отверстия на расстоянии 1,25м от него. Спектр источника содержит две длины волны 4000А и 6000А. Какой цвет увидит наблюдатель в точке А, находящейся на расстоянии 2,5м от отверстия. Радиус отверстия 1мм.
Задача 31.
С поверхности серого тела площадью S = 10см2 за 1 мин. излучается энергия W = 34,02 кДж. Коэффициент поглощения тела α = 0,625. Найти температуру тела и длину волны, на которую приходится максимум излучательной способности этого тела.
Задача 32.
Абсолютно черное тело, имеющее температуру 727 С, излучает с площади 20 см2 за промежуток времени 5 мин. такую же энергию, какую излучает второе абсолютно черное тело с площади 10 см2 за промежуток времени 2,5 мин. Определить длину волны, при которой излучательная способность второго тела максимальна?
Задача 35.
Какую энергию излучает за промежуток времени 10мин с поверхности 100см2 серое тело, коэффициент поглощения которого 0,5, если максимум излучательной способности приходится на длину волны 2,9•10-6м?
Задача 36.
Изменение в 1,5 раза частоты ультрафиолетового излучения, падающего на вещество с работой выхода 4 эВ, привело к увеличению задерживающей разности потенциалов в 2 раза. Найти энергию и импульс фотонов, падавших на вещество до изменения частоты света.
Задача 37.
Ультрафиолетовое излучение, длина волны которого 2,3*10(-7)м, падает на вещество и вызывает фотоэффект. При облучении другого вещества задерживающая разность потенциалов остается такой же, что и для первого вещества, если увеличить частоту излучения на величину 2*10(14) Гц. Длины волн, соответствующие красным границам этих веществ, отличаются в 1,25 раза. Найти максимальные энергию и скорость фотоэлектронов, выбиваемых из первого вещества.
Задача 41.
Кинетическая энергия электрона, выбитого фотоном из атома водорода, оказалась равна по модулю полной энергии этого электрона, которую он имел в атоме водорода. Найти энергию фотона, выбившего этот электрон. Длина волны де Бройля выбитого электрона
λБ = 6,645 Å.
Задача 42.
Электрон, находящийся на некотором энергетическом уровне в атоме водорода, может перейти в основное состояние одним из 4 различных способов через ниженаходящиеся энергетические уровни. Найти длину волны де Бройля электрона на исходном уровне и суммарную энергию фотонов, испущенных при таком переходе. Показать вышеупомянутые 4 перехода на энергетической диаграмме атома водорода.
|  |  | Методичка 2012 часть 2 |  |
| |
Федеральное агентство связи
Государственное образовательное учреждение
высшего профессионального образования
Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича
ФИЗИКА
Методические указания и контрольные задания(бакалавриат)
Факультет вечернего и заочного обучения
Часть II
Санкт-Петербург
2012
Готовые задачи по физике можно приобрести онлайн.
Стоимость одной готовой задачи по физике указана напротив каждой задачи.
Стоимость выполнения на заказ уточняйте при заказе.
Решение подробно расписано в формате Word. На почту высылаем файл word + копию в pdf.
Выполнены следующие задачи
(можно купить решенные ранее задания по физике онлайн и мгновенно получить на email)
По проводу длиной l = 10 м, площадь поперечного сечения которого S = 1 мм2, течет ток, плотность которого меняется со временем согласно выражению j = 12t2 А/см2. Концентрация электронов в проводе n = 2,5·1023 см-3, их подвижность μ = 10-3 м2/В·с. Найти: заряд, прошедший через сечение провода за промежуток времени от t1 = 0 до t2 = 4 c; количество теплоты Q, выделившееся в проводе за этот промежуток времени; скорость упорядоченного движения электронов V в момент времени t2 = 4 c.
Напряжение между концами проводника линейно возрастает со временем: U = 0,2t, B. Длина проводника 4 м, площадь его поперечного сечения 2 мм2. За одну минуту в проводе выделилось количество теплоты 36 Дж. Найти: удельное сопротивление ρ материала проводника; заряд, прошедший через поперечное сечение проводника за одну минуту, начиная с t1 = 0; плотность тока в проводнике через одну минуту после начала отсчета времени.
Скорость упорядоченного движения электронов в проводе меняется со временем согласно уравнению v = 4·10-5t, м/с. Удельное сопротивление металла 2,5·10-6 Ом·см, концентрация свободных электронов 2,5·1023 см-3, площадь поперечного сечения провода 5 мм2. Найти: заряд, прошедший через поперечное сечение провода за промежуток времени от 2 с до 4 c; напряженность электрического поля Е в проводе в момент времени, равный 2 с; зависимость удельной тепловой мощности тока w от времени.
Напряженность поля в проводнике меняется со временем согласно уравнению E = 1,6·10-3 В/м. Площадь поперечного сечения проводника 2 мм2, подвижность свободных электронов 3,5·10-3 м2/В·с. В момент времени, равный 3 с, плотность тока в проводе была равна 9·105 А/м2. Найти: концентрацию электронов в проводнике; заряд, прошедший через сечение проводника за промежуток времени от 0 до 3 c; зависимость удельной тепловой мощности тока w от времени.
В 10 см3 проводника за 5 минут выделилось количество теплоты равное 1,50 кДж при прохождении постоянного тока. Плотность тока в проводнике 1,0 А/мм2. Напряжение между концами проводника 50 В. Найти: удельную тепловую мощность тока; напряженность поля и силу тока в проводнике; заряд, прошедший через сечение проводника за 5 минут.
К источника тока с ЭДС ε = 12 В и внутренним сопротивлением r = 2 Ом присоединена катушка из провода длиной 40 м и поперечным сечением 2 мм2. Удельное сопротивление материала проводника 5⋅10-7 Ом⋅см. Найти: удельную тепловую мощность тока; плотность тока и напряженность поля в проводе; удельную тепловую мощность тока w в проводе и количество теплоты, выделяющееся в 1 см3 провода за одну минуту.
Напряжение между концами проводника меняется с течением времени: U = 2t, В. За промежуток времени от 0 до 3 с через поперечное сечение проводника прошел заряд 45 Кл. Длина проводника 10 м, подвижность свободных электронов в нем 10-3 м2/(В·с). Найти: количество теплоты, выделившееся за промежуток времени от 0 до 3 c; зависимость скорости упорядоченного движения электронов от времени.
К источнику тока с ЭДС ε = 5.5 В и внутренним сопротивлением r = 1 Ом подключили катушку с намотанным проводом длиной l = 20 м и площадью поперечного сечения S = 1 мм2. По цепи пошел ток I = 0.5 А. Найти: удельное сопротивление материала провода; напряженность и плотность тока в проводе; удельную тепловую мощность тока в проводе.
Удельная тепловая мощность тока в проводнике меняется со временем: w = 1.6⋅102 t2, Вт/м3. Концентрация свободных электронов в проводнике 2,5⋅1023 см-3; их подвижность 10-3 м2/(В⋅с). Найти: плотность тока и напряженность электрического поля в проводнике в момент времени, равный 5 с; количество теплоты, выделившееся в объеме 30 см3 проводника за первые 10 с.
Мощность тока, идущая на тепловые потери в проводнике объемом 200 см3, растет со временем: N = 0,05·t4, Вт. Концентрация свободных электронов в проводнике 2,5·1023 см-3, их подвижность 10-3 м2/(В·с). Найти: напряженность поля и скорость упорядоченного движения свободных электронов в проводнике в момент времени, равный 10 с; зависимость плотности тока от времени.
Электроны влетают в однородное магнитное поле под углом 60° к силовым линиям и движутся по винтовой траектории, радиус которой равен 0.34 cм. На сколько переместятся электроны вдоль силовых линий за 10 оборотов?
Протон (m = 1,67·10-27 кг, q = 1,6·10-19 Кл) движется в однородном магнитном поле по винтовой линии с радиусом 1 мм и шагом 5 мм. Индукция поля 0,1 Тл. Найти скорость протона и угол между ней и индукцией.
Протон (m=1.67⋅10-27 кг, q=1.6⋅10-19 Кл) влетает со скоростью v = 100 км/с в область пространства, где имеются электрическое (E = 210 В/м) и магнитное (B = 3.3 мТл) поля, совпадающие по направлению. Определить ускорение протона для двух случаев: 1) направление скорости совпадает с направлением полей; 2) направление скорости перпендикулярно направлению полей.
Заряженная частица прошла ускоряющую разность потенциалов 104 В и влетела в скрещенные под прямым углом электрическое (Е = 10 кВ/м) и магнитное (В = 0,1 Тл) поля. Найти отношение заряда частицы к её массе, если, двигаясь перпендикулярно обоим полям, частица не изменяет величины и направления скорости
Альфа-частица (масса m = 6,6·10-27 кг, заряд q = 3,2·10-19 Кл) движется в однородном магнитном поле с H = 9,5·105 А/м по окружности с R = 25 см в плоскости, перпендикулярной силовым линиям. Определить: скорость частицы; период обращения частицы по окружности.
Пластинка полупроводника толщиной а = 0,4 см помещена в магнитное поле, направленное вдоль а. Перпендикулярно полю вдоль пластинки течет ток I = 0,2 А. При этом возникает поперечная разность потенциалов U = 6 мВ (эффект Холла). Подвижность носителей тока 0,6 м2/В·с; удельное сопротивление полупроводника 10-5 Ом·м. Определить индукцию магнитного поля.
Через сечение S = a x b медной пластинки толщиной a = 0,5 мм и высотой b = 10 мм идет ток 20 А. При помещении пластинки в магнитное поле, перпендикулярное ребру b и направлению тока, возникает поперечная разность потенциалов 3,1 мкВ. Индукция магнитного поля 1 Тл. Определить: 1) концентрацию электронов в меди; 2) среднюю скорость направленного движения электронов.
На боковых гранях медной пластинки, помещенной в однородное магнитное поле с индукцией 0,32 Тл, в результате эффекта Холла возникает разность потенциалов 10-6 В. Длина пластинки 5·10-2 м, ширина 0,5 см, толщина 0,15 мм. Для меди концентрация электронов 8·1028 м-3, удельное сопротивление 1,7·10-8 Ом·м. Найти подвижность электронов и силу тока, текущего по пластинке.
В магнитное поле с индукцией 0,2 Тл помещена пленка шириной 2·10-3 м и толщиной 10-4 м, по которой протекает ток 4,8 А. Концентрация электронов в пленке 1029 м-3. Определить холловскую разность потенциалов и скорость упорядоченного движения электронов.
Пластинка полупроводника с удельным сопротивлением ρ = 10-5 Ом⋅м и толщиной a = 0.2 мм помещена в магнитное поле индукцией 1 Тл, направленное вдоль а. Вдоль пластинки перпендикулярно полю пропускается ток 0,1 А. При этом возникает поперечная разность потенциалов 3,25⋅10-3 В (эффект Холла). Определить подвижность носителей тока в полупроводнике.
По двум длинным параллельным проводам, расположенным на расстоянии 10 см один от другого, в одинаковых направлениях текут токи I1 = 2 А и I2. Индукция магнитного поля в точке, находящейся на расстоянии 10 см от каждого из проводов, B = 1,1·10-5 Тл . Определить силу тока во втором проводнике I2.
Длинный провод, согнутый под прямым углом, и круговой контур, состоящий из пяти витков, расположены в одной плоскости (рис. 1). Магнитный момент контура pm = 0.028 А⋅мм2 перпендикулярен плоскости чертежа. Центр кругового тока I2 находится на биссектрисе прямого угла. Радиус контура R = 6 см; a = 10 см; I1 = 10 А. Найти напряженность магнитного поля в центре кругового контура. Укажите направление тока I2.

Квадратный проводящий контур вписан в круговой проводящий контур (рис. 2). По круговому контуру течет ток 2 A, по квадратному - ток 3 A. Радиус кругового контура 20 см. Определить индукцию магнитного поля в точке О.

Квадратный контур и круговой контур с радиусом R = 5 см расположены во взаимно перпендикулярных плоскостях (рис. 3). Магнитный момент кругового контура 0,0314 А·м2. По квадратному контуру течет ток I1. Напряженность магнитного поля в центре системы (точка O) H0 = 54 A/м. Определить силу тока I1 в квадратном контуре.

Прямой бесконечный проводник имеет круговую петлю (рис. 4). По проводнику течет ток 5 А, напряженность магнитного поля в центре петли 41 А/м. Определить магнитный момент петли с током.

По длинному соленоиду течет ток 0,1 А. Радиус соленоида 2 см, линейная плотность витков 103 м-1. Внутри соленоида круговой виток радиусом 1 см расположен так, что ось соленоида проходит через плоскость витка и его центр. Ток витка 1 А. Найти величину напряженности магнитного поля в центре витка.
По длинному соленоиду течет ток 0,1 А. Радиус соленоида 2 см, линейная плотность витков 103 м-1. С осью соленоида совпадает ось провода с током 2 А. Найти напряженность поля в точке, находящейся на расстоянии 1 см от оси провода, отсчитываемом вдоль радиуса соленоида.
По бесконечному проводу течет ток 10А. В плоскости, перпендикулярной проводу, расположен контур в виде равностороннего треугольника с током 1А. Сторона треугольника 2см. Определить напряженность магнитного поля в центре контура, находящегося на расстоянии 5см от провода.
По бесконечному проводу течет ток 10 А. В плоскости, перпендикулярной проводу, расположен контур в виде кругового витка с током 1 А. Радиус витка 1 см, его центр находится на расстоянии 5 см от провода. Найти величину напряженности магнитного поля в центре витка.
По бесконечному проводу течет ток 10 А. В плоскости, перпендикулярной проводу, расположен контур в виде квадрата со стороной 2 см и током 1 А. Расстояние от центра квадрата до провода 5 см. Определить напряженность магнитного поля в центре квадрата.
Внутри длинного соленоида с плотностью витков n = 5 cм-1 находится рамка с площадью S0 = 10 см2 и числом витков N = 1000. Рамка равномерно вращается с частотой ν = 10 Гц относительно оси, лежащей в плоскости рамки и перпендикулярной силовым линиям магнитного поля соленоида. Ток в соленоиде I1 = 2 A, сопротивление рамки R = 5 Ом. Определить: силу тока I2 в рамке в момент времени t2 = T/4 c; заряд, прошедший по рамке за промежуток времени от t1 = 0 до t2.
Круговой проводящий контур находится в однородном магнитном поле, индукция которого меняется во времени по закону B = 5⋅10-3t2, Тл. Радиус контура r = 2 см. Сопротивление контура R = 10 Ом. Угол между направлением вектора B и плоскостью контура α = 30°. Найти: 1) заряд, прошедший по контуру за промежуток времени от t1 = 2 c до t2 = 4 c; 2) ток в контуре в момент времени t2.
Внутри длинного соленоида с линейной плотностью витков n = 20 см-1 расположена прямоугольная рамка, состоящая из пяти витков со сторонами 7 см и 10 см. Нормаль к рамке составляет угол α = 45° с силовыми линиями магнитного поля. По соленоиду течет ток, изменяющийся во времени по закону I = 0,04t2, А. Сопротивление рамки R = 2 Ом. Определить: 1) индукционный ток в рамке в момент времени t’ = 3 с; 2) заряд, прошедший по рамке за промежуток времени от t1 = 2 c до t2 = 4 c.
Рамка площадью 100 см2 содержит 103 витков провода сопротивлением R1=12 Ом. К концам обмотки подключено внешнее сопротивление R2=20 Ом. Рамка равномерно вращается в однородном магнитном поле (B=0.1 Тл), делая оборотов в секунду. Ось вращения лежит в плоскости рамки и перпендикулярна силовым линиям магнитного поля. Чему равно максимальное значение мощности переменного тока в цепи?
Бесконечно длинный прямой провод с током I и прямоугольный контур расположены так, как показано на рис. 5. При выключении тока в проводе по контуру протекает заряд 2,1·10-8 Кл. Определить начальное значение тока в проводе. Показать направление индукционного тока в контуре. Сопротивление контура 2 Ом.

Две катушки имеют взаимную индуктивность L12 = L21 = 5 мГн. В первой катушке сила тока изменяется по закону I1(t) = 10sin100πt, А. Найти 1) максимальное значение ЭДС, индуцируемой во второй катушке; 2) силу тока I2 во второй катушке в момент времени t' = T/6. Сопротивление второй катушки 5 Ом.
Взаимная индуктивность двух контуров L12 = L21 = 0,05 Гн. При изменении тока I1 в первом контуре во втором возникает ЭДС, которая изменяется во времени по закону ε2 = 0,5t, В. Найти: 1) силу тока I1 в первом контуре в момент времени t2 = 2 c; Магнитный поток ψ2, сцепленный со вторым контуром в момент времени t2, считая, что при t1 = 0 ψ2 = 0.
По длинному прямому проводу течет ток, изменяющийся со временем по закону I = 0,3t2+1, А. В одной плоскости с проводом расположен прямоугольный контур (рис. 5), где: а = с = 20 см, b = 30 см. Определить: 1) взаимную индуктивность провода и контура; 2) ЭДС, индуцируемую в контуре в момент времени, равный 3 с.

По длинному прямому проводу течет ток I1=1 А. По квадратному контуру течет ток I2 (рис. 6). Контур удаляется за пределы действия магнитного поля провода. При этом совершается работа A=42нДж. b=10 см, a=30 см. Определить ток во втором контуре I2, а также взаимную индуктивность провода и контура.

Соленоид имеет 1,2·104 витков. Длина соленоида 60 см, радиус витков 4 см. Сверху на соленоид надета катушка из 10 витков, расположенная в его середине. Длина катушки значительно меньше длины соленоида. Определить взаимную индуктивность катушки и соленоида.
По круговому контуру с число витков 10 и радиусом 4 см течет ток I. Магнитный момент контура 0,1 А·м2. Плоскость контура составляет угол α1 = 30° с линиями однородного магнитного поля с индукцией 0,126 мТл. Определить: напряженность магнитного поля в центре контура; работу, совершаемую при повороте контура из заданного положения в положение, при котором угол между плоскостью контура и направлением силовых линий магнитного поля α2 = 60°.
Рамка, длиной a = 5 см и шириной b = 2 см, содержащая N = 200 витков проволоки, находится в однородном магнитном поле с индукцией B = 0.1 Тл. Плоскость рамки составляет угол α = 30° с направлением вектора магнитной индукции. По рамке течет ток I = 2 мА. Определить: магнитный момент рамки; вращающий момент, действующий на рамку; работу, совершаемую при удалении рамки за пределы действия магнитного поля.
По длинному соленоиду с плотностью витков n = 20 см-1 течет ток I1 = 0,5 А. Внутри соленоида расположен квадратный контур из 10 витков. Сторона контура a = 3 см. Магнитный момент контура pm = 2,7·10-3 А·м2. Плоскость составляет угол 30° с силовыми линиями магнитного поля соленоида. Определить: силу тока I2 в контуре; вращающий момент, действующий на контур; работу, совершаемую при повороте контура в положение, при котором магнитный поток максимален.
Квадратный контур и длинный прямой провод расположены в одной плоскости (рис. 6). Магнитный момент контура pm=0.04 А⋅м2, I1=3А, a=b=10 см. Контур поворачивают на 180° вокруг оси, параллельной току I1 и проходящей через середину контура. Определить совершенную при повороте работу.

Длинный прямой провод и прямоугольный контур расположены, как показано на рис. 7. Контур перемещается из положения, в котором b = 5 см, в положение, в котором b = 10 см. При этом совершается работа 23 нДж. Ток I1 = 2 A, c = 5 см, а = 10 см. Определить I2.

По катушке с индуктивностью L = 0,1 Гн и сопротивлением R = 20 Ом течет ток I0 = 5 А . Источник тока можно отключить, не разрывая цепи. Определить энергию магнитного поля катушки через Δt = 0,01 с после отключения источника.
Соленоид индуктивностью 0,2 Гн и сопротивлением 2·10-2 Ом замыкается на источник, ЭДС которого 2 В, а внутреннее сопротивление ничтожно мало. Какой заряд пройдет через соленоид за первые 5 с после замыкания?
По соленоиду с индуктивностью L = 0.1 Гн и сопротивлением R = 10 Ом течет постоянный ток. Концы соленоида отсоединяют от источника и замыкают накоротко. За какой промежуток времени в соленоиде выделится количество теплоты, равное половине первоначального значения энергии магнитного поля соленоида?
Длинный соленоид содержит 800 витков с радиусом 2,5 см, Длина соленоида 40 см. Сила тока в соленоиде меняется со временем по закону I(t) = 5sin(π/2)t, А. Определить: индуктивность соленоида, максимальные значения напряженности магнитного поля в соленоиде и магнитного потока, сцепленного с витками соленоида, ЭДС самоиндукции и объемную плотность энергии магнитного поля в момент времени, равный 0,5 с.
При изменении силы тока в контуре по закону I = 5t2 + 2, А, в нем возникает ЭДС, которая в момент времени равный t1 = 2с равна 2 В. Определить энергию магнитного поля W1 в этот момент.
Материальная точка совершает колебания по закону x = 5sin2t, см. Максимальная сила, действующая на точку, равна 4⋅10-3 Н. Определить: массу материальной точки, полную энергию точки и путь, пройденный точкой за 10 полных колебаний.
Амплитуда гармонических колебаний материальной точки массой 40 г равна 2·10-2 м. Максимальная скорость 0,1 м/с. Написать уравнение колебаний, считая, что в начальный момент времени смещение от положения равновесия равно половине амплитуды. Определить силу, действующую на материальную точку, в момент времени t1 = Т/3.
Период гармонических колебаний материальной точки равен 8,0 с. Масса 5,0 г. Написать уравнение колебаний точки x(t). За начало отсчета времени принять момент времени, когда отклонение от положения равновесия положительно и равно максимальному значению 4,0 см. Определить: силу, действующую на точку, кинетическую и потенциальную энергии точки в момент времени t1 = T/3.
Полная энергия тела, совершающего гармонические колебания, 4·10-4 Дж; максимальное значение силы, действующей на тело, 2·10-2 Н; частота колебаний 0,5 Гц; начальная фаза колебаний 60°. Написать уравнение колебаний тела. Определить максимальные значения скорости и ускорения тела.
Материальная точка совершает гармоническое колебание по закону x = 4sin(0.2πt + π/3) . Её полная энергия равна 1,8·10-5 Дж. Определить массу материальной точки.
Колебательный контур состоит из катушки индуктивности 1,6 мГн и конденсатора ёмкостью 0,04 мкФ. Сопротивление контура ничтожно мало. Максимальное напряжение на конденсаторе 200 В. Написать законы изменения заряда на обкладках конденсатора и силы тока в контуре с течением времени. Определить энергию электрического и энергию магнитного поля в момент времени t1 = T/12.
Период незатухающих колебаний в колебательном контуре равен 10-3 с. Амплитудное значение силы тока равно 0,40 А, индуктивность катушки 0,05 Гн. Определить емкость конденсатора. Написать закон изменения напряжения на обкладках конденсатора с течением времени. Определить энергию электрического поля в тот момент, когда сила тока равна половине максимального значения. Сопротивлением контура пренебречь.
Колебательный контур состоит из катушки индуктивностью 0,40 Гн, и конденсатора емкостью 2,5 мкФ. Полная энергия контура 2⋅10-6 Дж. Написать закон изменения силы тока и разности потенциалов на обкладках конденсатора со временем, считая, что в начальный момент времени заряд на конденсаторе максимальный. Сопротивлением контура пренебречь.
Разность потенциалов на обкладках конденсатора в колебательном контуре изменяется по закону U = 20sin(103t), В. Индуктивность контура равна L = 2.5 Гн. Определить емкость контура и написать законы изменения с течением времени энергии электрического поля и энергии магнитного поля контура. Сопротивлением контура пренебречь.
Сила тока в колебательном контуре, состоящем из последовательно соединенных катушки индуктивностью 2,0 Гн и конденсатора, изменяется со временем по закону I = 5·10-3sin(2·103t), А. Определить емкость контура, период колебаний в контуре, энергию электрического и магнитного полей в момент времени t1 = T /2. Сопротивлением контура пренебречь.
Уравнение затухающих колебаний материальной точки массой 20 г имеет вид: x = 4·10-12·e-0,2tcos(π/4)t, м. Определить: коэффициент упругости, коэффициент сопротивления, собственную частоту колебаний, логарифмический декремент затухания и амплитуду колебаний после двух полных колебаний.
Период затухающих колебаний материальной точки 4,0 с. Логарифмический декремент затухания θ = 1.6. В начальный момент времени смещение от положения равновесия максимально и равно x0=xmax. Написать уравнение колебаний. За какое время амплитуда колебаний уменьшается на 20% от первоначального значения?
Отклонение от положения равновесия материальной точки массой 200 г происходит по закону: x = 2·10-2·e-0,1t·cos(0,2t) м. Определить: собственную частоту колебаний, коэффициент упругости, логарифмический декремент затухания и время, за которое амплитуда колебаний уменьшится в 5 раз.
В начальный момент времени смещение колеблющейся точки максимально и равно 8см. За 5 колебаний амплитуда уменьшается на 25% своей первоначальной величины. Период колебаний равен 0,5 с. Определить коэффициент затухания и логарифмический декремент колебаний. Написать уравнение колебаний.
Дата выполнения: 2023/07/03
Груз массой 0.40 кг прикреплен к пружине, коэффициент упругости которой равен 200 Н/м. Вынуждающая сила изменяется по закону F = 2·sin20t, Н. Написать уравнение установившихся вынужденных колебаний, если известно, что коэффициент сопротивления равен 0,20 кг/с.
Значения параметров колебательного контура следующие: С = 1,0·10-6 Ф, L = 0,5 Гн, R = 40 Ом. Амплитуда напряжения на обкладках конденсатора 10 В. Определить: период колебаний, коэффициент затухания, добротность контура. На сколько процентов частота свободных колебаний контура отличается от собственной частоты контура? Написать закон изменения напряжения на конденсаторе с течением времени.
Колебательный контур состоит из катушки индуктивности 0,20 Гн, двух параллельно соединенных конденсаторов емкостью 4,0 мкФ каждый и омического сопротивления 20 Ом. Начальное напряжение на конденсаторах 20 В. Определить период колебаний в контуре; логарифмический декремент затухания; число колебаний, после которых амплитуда напряжения уменьшается в 10 раз.
В последовательном электрическом контуре, содержащем омическое сопротивление, катушку индуктивностью 1.0 Гн и конденсатор, происходят затухающие колебания. При этом напряжение на обкладках конденсатора изменяется со временем по закону: UC=30⋅e-1000tcos(103t), В. Определить коэффициент затухания, собственную циклическую частоту колебаний, ёмкость и омическое сопротивление контура. Чему равен начальный заряд на обкладках конденсатора?
В исходном положении ключа происходит заряд конденсатора ёмкостью 4,0 мкФ от источника постоянного напряжения до 20 В. В другом положении конденсатор отключен от источника и разряжается через катушку индуктивностью 2,5 Гн с сопротивлением 25 Ом. Нарисовать схему опыта. Вычислить коэффициент затухания, циклическую частоту колебаний. Написать, как изменяется заряд конденсатора с течением времени, считая за начало отсчета времени момент переключения ключа.
Колебательный контур состоит из катушки индуктивностью L = 0,40 Гн, конденсатора емкостью C = 4,0 мкФ и сопротивления R = 160 Ом. Начальный заряд на конденсаторе равен q0 = 8,0·10-5 Кл. Написать закон изменения со временем напряжения на обкладках конденсатора. Определить логарифмический декремент затухания.
Материальная точка участвует в 2-х колебаниях равных частот и амплитуд и происходящих в одном направлении. Период равен 2 с. Амплитуды равны 3 см. Различаются колебания только начальными фазами, которые равны: π/2 и 0. Написать уравнение результирующего колебания и сделать рисунок с векторным представлением колебаний.
Материальная точка участвует в 2-х колебаниях равных частот и амплитуд и происходящих в одном направлении. Период равен 4,0 с. Амплитуды равны 5,0 см. Различаются колебания только начальными фазами, которые равны: π/2 и π. Написать уравнение результирующего колебания и сделать рисунок с векторным представлением колебаний.
Материальная точка участвует в 2-х колебаниях равных частот и амплитуд и происходящих в одном направлении. Период равен 8,0 c. Амплитуды равны 6 см. Различаются колебания только начальными фазами, которые равны: 0 и - π/2. Написать уравнение результирующего колебания и сделать рисунок с векторным представлением колебаний.
Материальная точка участвует в 2-х колебаниях происходящих в одном направлении. Частоты колебаний равны 20 Гц. Амплитуда первого колебания равна 3,0 см; второго – 4,0 см. Начальная фаза первого колебания – 0; второго – п/2. Написать уравнение результирующего колебания и сделать рисунок с векторным представлением колебаний.
Материальная точка массой 0,20 кг участвует в 2-х одинаково направленных колебаниях. Уравнения колебаний: x1 = 4cos(3t+0,4π); x2 = 3cos(3t+0,9π), мм. Написать уравнение результирующего колебания. Определить полную энергию материальной точки.
Движение материальной точки в результате сложения 2-х взаимно перпендикулярных гармонических колебаний одинаковых частот, амплитуд и отличающихся фазами колебаний на π/2 происходит по окружности радиусом 5 см с постоянной скоростью 10 см/с по часовой стрелке. Вычислить амплитуду, частоту колебаний и написать уравнения колебаний x(t) и y(t) в явном виде.
Движение материальной точки в результате сложения 2-х взаимно перпендикулярных гармонических колебаний одинаковых частот, амплитуд и отличающихся фазами колебаний на π/2 происходит по окружности радиусом r = 10 см с постоянной скоростью 5 см/с против хода часовой стрелки. Вычислить амплитуду, частоту колебаний и написать уравнения колебаний x(t) и y(t) в явном виде.
На горизонтально и вертикально отклоняющие пластины осциллографа подаются напряжения:
UX = 20cosπt, В; UY = 10cos(πt + ϕ0), В.
Чувствительность пластин одинакова и равна 1 мм/В. Написать уравнение траектории, по которой движется точка от электронного луча на экране осциллографа, для двух случаев: а) ϕ0 = 0; б) ϕ0 = π/2.
На горизонтально и вертикально отклоняющие пластины осциллографа подаются напряжения приводящие к отклонению электронного луча по закону x(t)=80cos25t, мм по горизонтали и y(t)=20sin25t, мм по вертикали. Написать уравнение траектории, наблюдаемой на экране осциллографа. Определить скорость точки от электронного луча на экране в момент времени, когда x=0.
На горизонтально и вертикально отклоняющие пластины осциллографа подаются напряжения приводящие к отклонению электронного луча по закону x(t) = 4·cos(2,5t), мм по горизонтали и y(t) = 2,5·sin(2,5t), мм по вертикали. Написать уравнение траектории, наблюдаемой на экране осциллографа. Определить скорость точки от электронного луча на экране в момент времени, когда y = 0.
Уравнение незатухающих колебаний дано в виде x = 4sinπt, см. Найти смещение от положения равновесия точки, находящейся на расстоянии 75 см от источника колебаний, через 0,01 с после начала колебаний. Скорость распространения колебаний 300 м/с.
Уравнение незатухающих колебаний дано в виде x = sin2,5πt, см. Найти смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии 20 м от источника колебаний, для момента t1 = 1 с после начала колебаний. Скорость распространения колебаний 100 м/с.
Какую разность фаз будут иметь колебания двух точек, находящихся на расстоянии соответственно 10 и 16 м от источника колебаний? Период колебаний 0,04 с, скорость распространения колебаний 300 м/с.
Найти смещение от положения равновесия точки, отстоящей от источника колебаний на расстоянии x1=λ/12 для момента t1=T/6. Амплитуда колебаний 0.05 м.
Смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника колебаний, в момент t1 = T/6 равно половине амплитуды. Найти длину бегущей волны.
В стальном стержне распространяется бегущая продольная волна от источника, уравнение колебаний которого дано в виде: x = 10-5sin(102t), м. Модуль Юнга стали E = 2⋅1011 Н/м2 ; плотность стали ρ = 8⋅103 кг/м3 . Написать уравнение волны. Определить: длину волны; максимальную относительную деформацию в стержне.
Уравнение незатухающих колебаний имеет вид: x = 10-6sin102t, м. Длина волны 15 м. Написать уравнение плоской волны. Определить: смещение точки среды, находящейся на расстоянии 20 м от источника в момент времени 0,01 с; разность фаз колебаний точек, расположенных на расстоянии 15 м и 20 м от источника.
Уравнение плоской волны, распространяющейся в стержне сечением 10 см2, имеет вид: ε = 6·10-6cos(1900t-5,7x) м. Определить: частоту колебаний, длину волны; скорость распространения волны в стержне. Какую энергию переносит волна через сечение стержня за 2 с? Плотность материала стержня 4·103 кг/м3.
Плоская бегущая акустическая волна представлена уравнением ξ(x,t)=5⋅104⋅sin(1980t - 6x), м. Определить: частоту колебаний; скорость и длину волны; максимальную относительную деформацию среды.
Уравнение незатухающих колебаний источника имеет следующий вид: x = 10-4sin100t, см. Длина волны 20 м. Написать уравнение плоской волны. Определить ускорение точки, находящейся на расстоянии 25 м от источника, в момент времени, равный 0,2 с.
|
|





